Posted on

Mayor 2023: Back of the Envelope

As the Mayor’s race heats up, I’m doing a series establishing some baseline numbers. What follows are simplistic calculations using reasonable assumptions. Welcome to the Back of the Envelope.

Breaking down the electorate

How many voters should we expect?

View code 
library(tidyverse)
library(sf)

source("../../admin_scripts/util.R")


setwd("C:/Users/Jonathan Tannen/Dropbox/sixty_six/posts/council_ballot_position_23/")

df_major_type <- readRDS("../../data/processed_data/df_major_type_20230116.Rds")
df_major <- df_major_type %>%
  group_by(office, candidate, party, warddiv, year, election_type, district, ward, is_topline_office) %>%
  summarise(votes = sum(votes))

df_major <- df_major %>% 
  group_by(year, election_type, office, district, warddiv) %>%
  mutate(pvote = votes / sum(votes)) %>%
  ungroup()

topline_votes <- df_major %>% 
  filter(is_topline_office) %>%
  group_by(election_type, year) %>%
  summarise(votes = sum(votes)) %>%
  mutate(
    year = asnum(year),
    cycle = case_when(
      year %% 4 == 0 ~ "President",
      year %% 4 == 1 ~ "District Attorney",
      year %% 4 == 2 ~ "Governor",
      year %% 4 == 3 ~ "Mayor"
    )
  )

cycle_colors <- c("President" = strong_red, "Mayor" = strong_blue, "District Attorney" = strong_green, "Governor" = strong_orange)

ggplot(
  topline_votes,
  aes(x=year, y=votes, color=cycle)
) +
  geom_line(size=1) +
  geom_point(size=2) +
  geom_text(
    data = tribble(
      ~votes, ~cycle,
      680e3, "President",
      580e3, "Governor",
      320e3, "Mayor",
      90e3, "District Attorney"
    ) %>% mutate(election_type = "general"),
    aes(label=cycle),
    x = 2022,
    hjust=1,
    fontface="bold"
  ) +
  theme_sixtysix() +
  expand_limits(y=0) +
  scale_y_continuous(
    "Votes cast in topline office" , 
    labels=scales::comma
  ) +
  scale_color_manual(
    values = cycle_colors,
    guide=FALSE
  )+
  facet_grid(~format_name(election_type)) +
  labs(
    x=NULL,
    title="Votes cast in Philadelphia elections"
  )

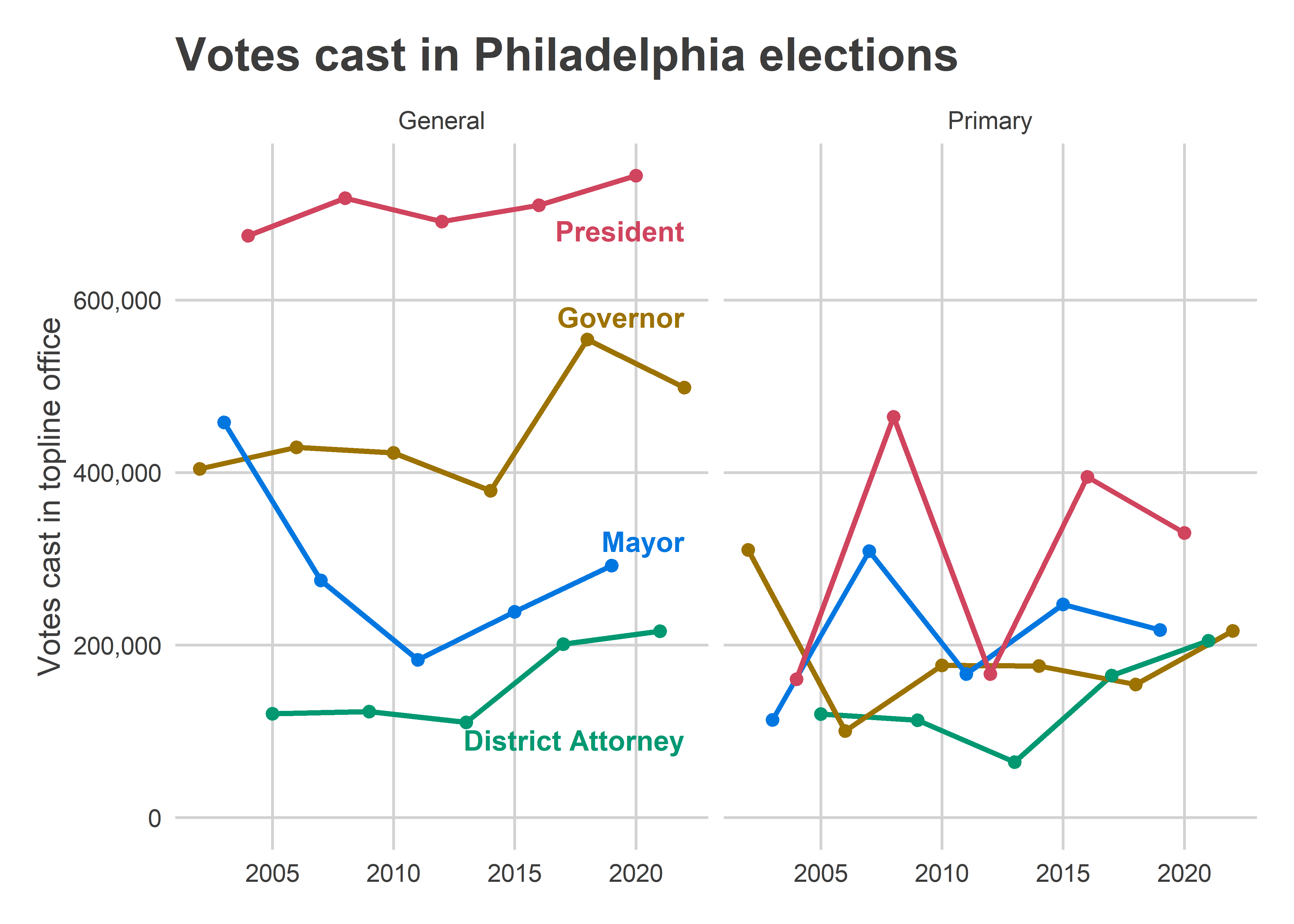
Mayoral primaries usually see the second highest turnout, after Presidential. In the last two competitive mayoral races, 2007 and 2015, we saw 309,000 and 247,000 votes respectively. Given that turnout has dramatically jumped post-2016 and this race is shaping up to be hyper competitive, I’d expect turnout around that 310,000 mark or higher.

How many votes will it take to win?

With so many candidates, the winner won’t need a very high percentage. The two most competitive recent, many-candidate races were 2007 Mayor and 2017 D.A., both with seven candidates. In 2007, Michael Nutter beat Thomas Knox 37% to 25%. In 2017, Larry Krasner beat Joe Khan 38% to 20%. So it looks like it took ~30% to win (halfway between first and second). I’ll call this number the “Win Percent”.

View code 
comp_elections <- tribble(
  ~year, ~election_type, ~office,
  "2009", "primary", "DISTRICT ATTORNEY",
  "2017", "primary", "DISTRICT ATTORNEY",
  "2015", "primary", "MAYOR",
  "2007", "primary", "MAYOR",
  "2020", "primary", "PRESIDENT OF THE UNITED STATES",
  "2008", "primary", "PRESIDENT OF THE UNITED STATES",
  "2004", "primary", "PRESIDENT OF THE UNITED STATES",
  "2022", "primary", "UNITED STATES SENATOR",
  "2016", "primary", "UNITED STATES SENATOR",
  "2010", "primary", "UNITED STATES SENATOR",
  "2006", "primary", "UNITED STATES SENATOR",
)

winnum_df <- df_major %>% inner_join(comp_elections) %>% 
  filter(
    ifelse(election_type == "primary", party == "DEMOCRATIC"),
    candidate != "Write In"
  ) %>%
  group_by(year, election_type, office, candidate) %>%
  summarise(votes = sum(votes)) %>%
  group_by(year, election_type, office) %>%
  mutate(
    pvote = votes / sum(votes),
    rnk = rank(desc(votes))
  ) %>%
  summarise(
    ncand = length(unique(candidate)),
    winner_pvote = pvote[rnk == 1],
    second_pvote = pvote[rnk == 2]
  ) %>%
  mutate(office_pretty = case_when(
    office == "PRESIDENT OF THE UNITED STATES" ~ "President",
    office == "UNITED STATES SENATOR" ~ "Senate",
    TRUE ~ format_name(office)
  ))

# df_major %>% 
#   filter(election_type == "primary", party == "DEMOCRATIC") %>%
#   filter(office == "MAYOR") %>%
#   group_by(year, candidate) %>%
#   summarise(votes = sum(votes))

ggplot(winnum_df, 
       aes(x=ncand, y=100*(winner_pvote + second_pvote) / 2)
) +
  geom_point(size=3, color = strong_purple) +
  ggrepel::geom_text_repel(aes(label=paste(year, office_pretty))) +
  theme_sixtysix() +
  expand_limits(y=0, x=c(1,8)) +
  labs(
    title = "With 10+ candidates, the win number could be < 25%",
    subtitle = "Philadelphia Democratic Primaries",
    x = "Number of candidates",
    y = "Win Percent\navg(first place, second place)"
  )

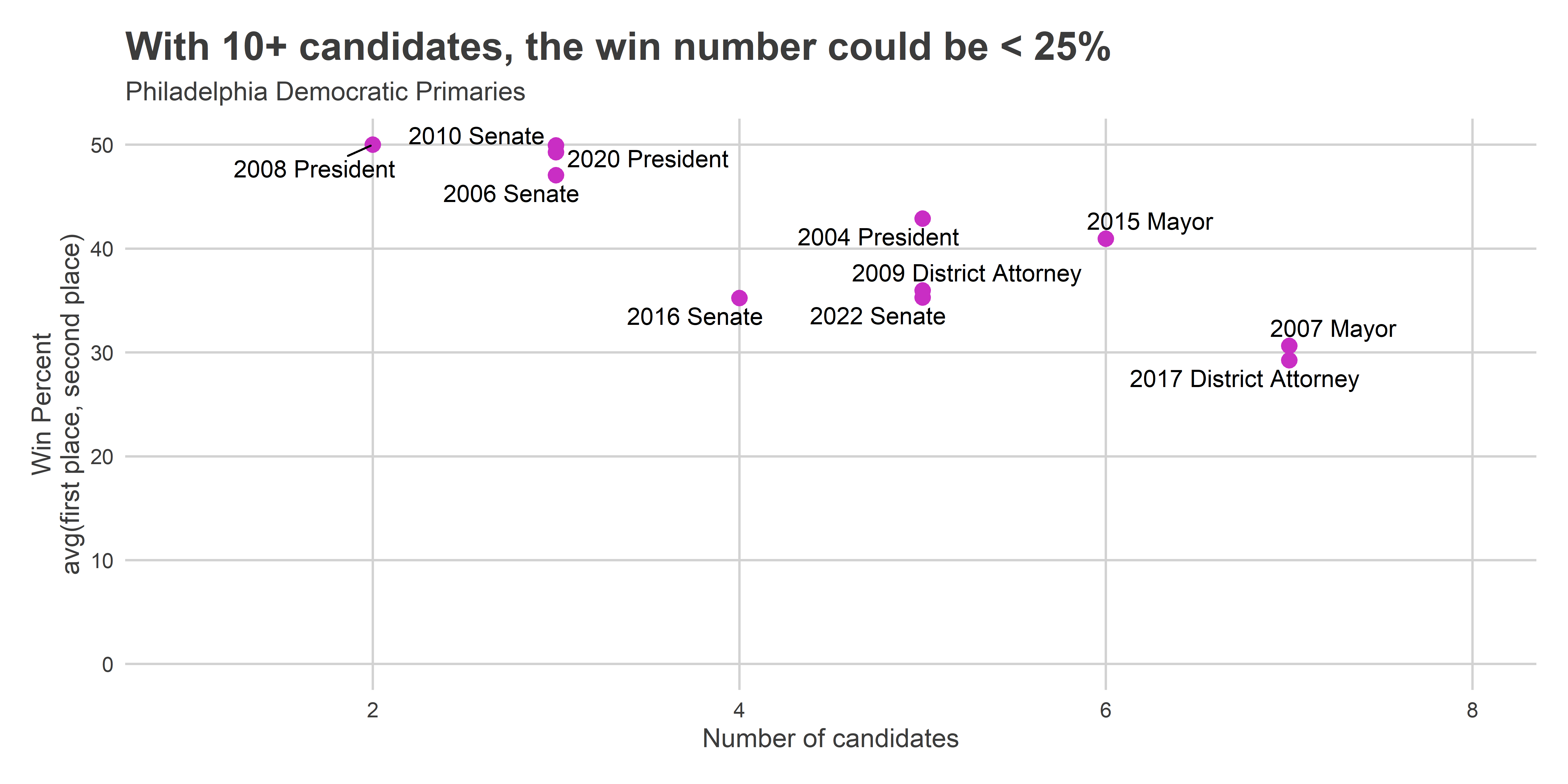
The win percentage at ten candidates looks like it will be 25%, or lower. We haven’t seen 10 candidates in a recent election. If we’re still at or above 10 come May, especially with such high-profile names, that win percent could be as low as 20%.

Where will those votes come from?

Division across the city turn out or stay home in patterns. I’ve analysed these patterns before, creating my voting blocs.

View code 
divs <- st_read("../../data/gis/warddivs/202011/Political_Divisions.shp") %>%
  mutate(warddiv = pretty_div(DIVISION_N))source("../../data/prep_data/div_svd_time_util.R")
div_cat_fn <- readRDS("../../data/processed_data/svd_time_20230116.RDS")

div_cats <- div_cat_fn %>% get_row_cats(2017) %>% rename(warddiv = row_id)

cats <- c(
  "Black Voters",
  "Wealthy Progressives",
  "Hispanic Voters",
  "White Moderates"
)

cat_colors <- c(light_blue, light_red, light_orange, light_green)
names(cat_colors) <- cats

ggplot(
  divs %>% left_join(div_cats, by="warddiv")
) +
  geom_sf(aes(fill=cat), color=NA) +
  scale_fill_manual(NULL, values=cat_colors) +
  theme_map_sixtysix() + #%+replace%
  # theme(legend.position="bottom", legend.direction="horizontal") +
  ggtitle("Philadelphia's Voting Blocs")

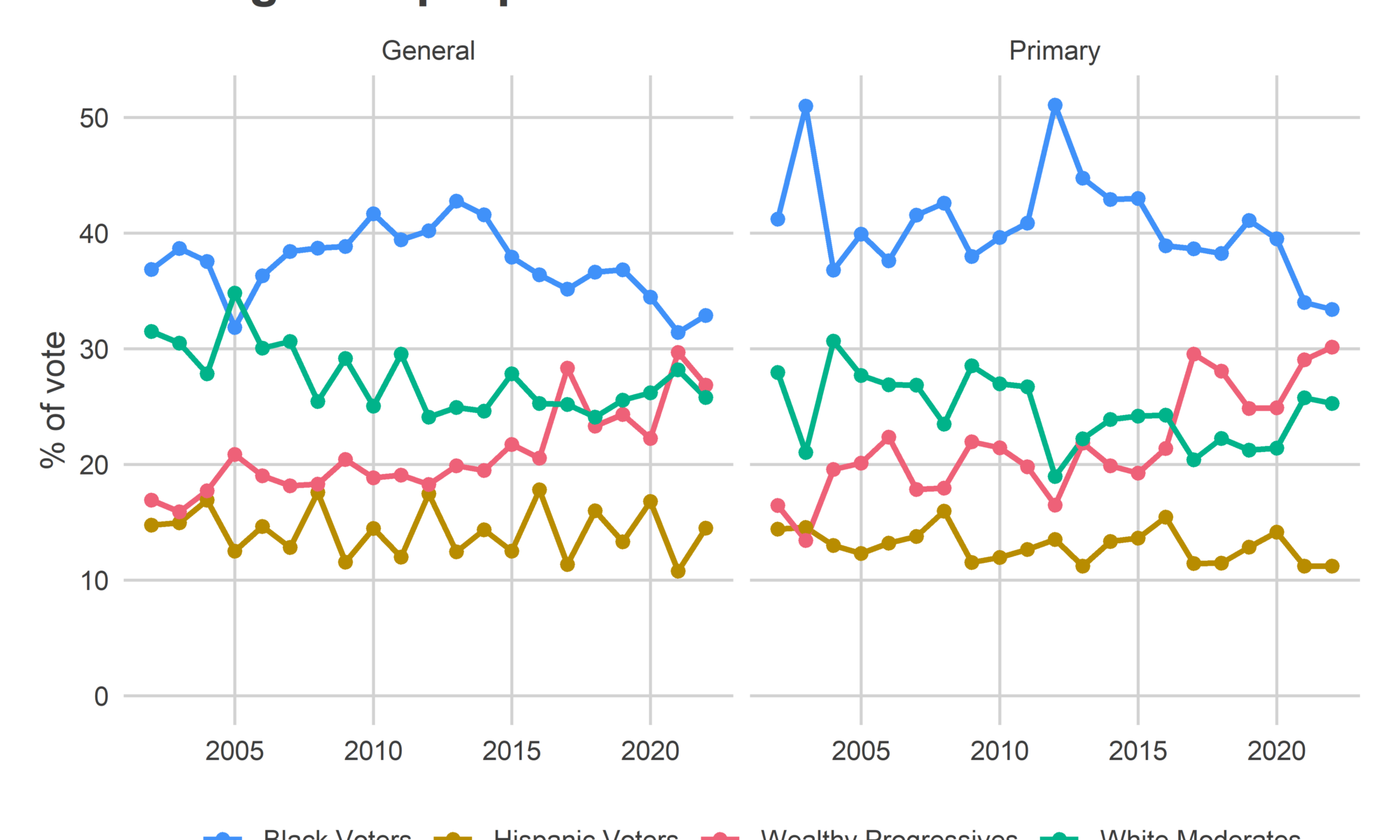
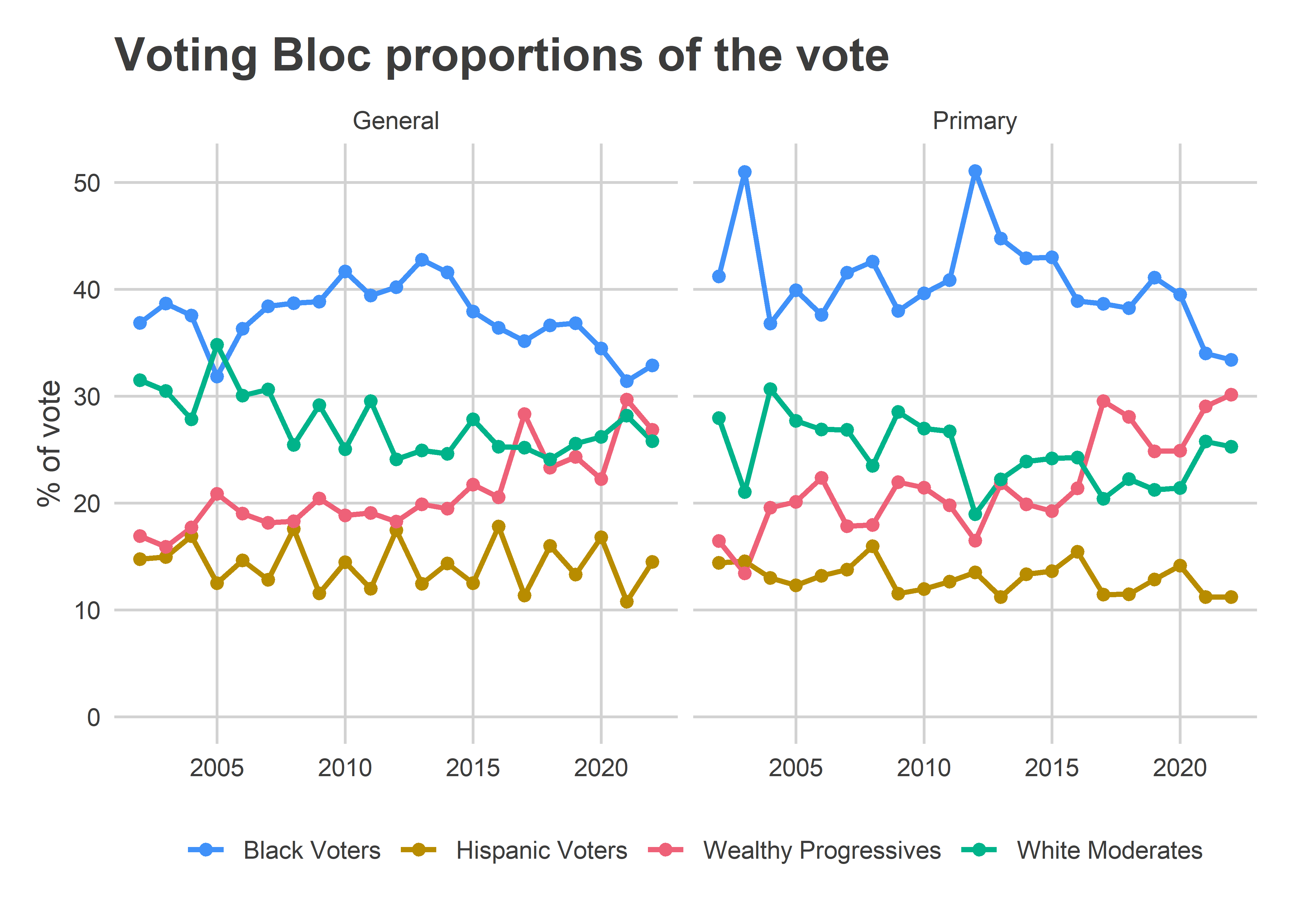
Philadelphia’s Black Wards have had a relatively low proportion of the vote since November 2020. But I expect that to recover a little in a Mayoral primary. Let’s say Black Voter divisions will cast more than 35% of votes, Wealthy Progressives about 30% of the vote, White Moderates 25%, and Hispanic North Philly 10%.

View code 
df_major %>%
  filter(is_topline_office) %>%
  left_join(div_cats %>% select(-year), by = "warddiv") %>%
  group_by(year, election_type, cat) %>%
  summarise(votes = sum(votes)) %>%
  group_by(year, election_type) %>%
  mutate(total_votes = sum(votes), pvote = votes / total_votes) %>%
  ungroup() %>%
  filter(!is.na(cat)) %>%
  ggplot(
    aes(x = asnum(year), y = 100*pvote, color=cat)
  ) +
  geom_line(size=1) +
  geom_point(size=2) +
  facet_grid(~format_name(election_type)) +
  theme_sixtysix() +
  scale_color_manual(NULL, values=cat_colors[order(names(cat_colors))]) +
  expand_limits(y=0) +
  labs(
    x = NULL,
    y = "% of vote",
    title = "Voting Bloc proportions of the vote"
  )

The types of possible winners

What kinds of coalitions could put a candidate over the top? Let’s assume a candidate (a) needs 25% of the vote to win, and (b) the breakdown of votes is 35% Black Voter divisions, 30% Wealthy Progressive divisions, 25% White Moderate divisions, and 10% Hispanic Voter divisions.

The winner will be the candidate who achieves \[ 0.35 p_{blk} + 0.30 p_{wprog} + 0.25 p_{wmod} + 0.10 p_{hisp} \ge 0.25, \] where \(p_i\) is the proportion of the vote received in bloc \(i\).

Consider, for example, just the Black Voter and Wealthy Progressive Blocs.

View code 
cat_corr_df <- df_major %>% 
  inner_join(winnum_df) %>%
  filter(candidate != "Write In", party == "DEMOCRATIC") %>%
  mutate(winnum = (winner_pvote + second_pvote)/2) %>%
  left_join(div_cats %>% select(-year)) %>%
  filter(!is.na(cat)) %>%
  group_by(year, office_pretty, candidate, cat, winnum) %>%
  summarise(votes = sum(votes)) %>%
  group_by(year, office_pretty, cat) %>%
  mutate(total_votes = sum(votes)) %>%
  ungroup() %>%
  mutate(
    pvote = votes / total_votes,
    pvote_norm = pvote / winnum
  ) %>%
  pivot_wider(
    id_cols = c(year, office_pretty, candidate, winnum),
    values_from = c(pvote, pvote_norm, votes),
    names_from = c(cat)
  )

y_prop <- 0.35
x_prop <- 0.30

ggplot(
  cat_corr_df,
  aes(
    x=`pvote_norm_Wealthy Progressives`, 
    y=`pvote_norm_Black Voters`
  )
) +
  geom_hline(yintercept = 1.0, color="grey50") +
  geom_vline(xintercept = 1.0, color="grey50") +
  geom_abline(slope = -x_prop / y_prop, intercept = 1 + x_prop/y_prop, linetype="dashed") +
  annotate(
    "text",
    label = "Win Line", 
    x=0.05, y=1 +x_prop/y_prop, 
    angle= atan(-x_prop / y_prop) * 180 / pi
  ) +
  geom_text(
    aes(label = paste0(format_name(candidate)," ", year)),
    size=3.0
  ) +
  coord_fixed() +
  theme_sixtysix() +
  labs(
    title="Candidate performance in\n Black and Progressive Divisions",
    x = "% of vote in Wealthy Progressive / Win Percent",
    y = "% of vote in Black Voter / Win Percent"
  )

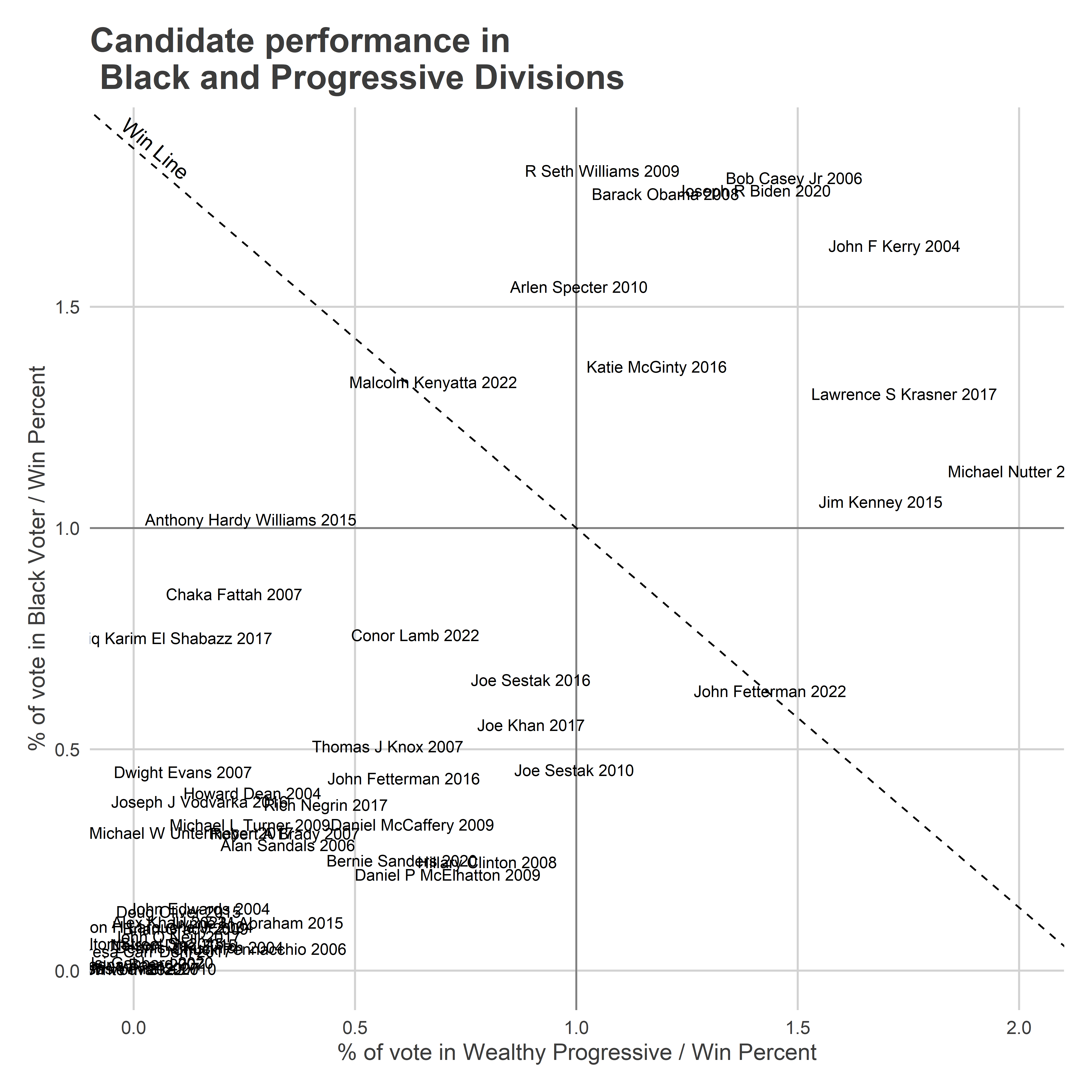
Winning these combined blocs requires being above the dashed line. Williams, Obama, Biden, Kerry, Krasner, Nutter, and Kenney all cleared it easily. Malcolm Kenyatta won these Philadelphia blocs in 2022 by dominating the Black Wards. Fetterman did better in the Wealthy Progressive wards, but not enough to win the head-to-head.

Compare that to the White Moderate and Black Voter comparison. These dimensions are uncorrelated; candidates often do well in one but not the other.

View code 
y_prop <- 0.35
x_prop <- 0.25

ggplot(
  cat_corr_df,
  aes(
    x=`pvote_norm_White Moderates`, 
    y=`pvote_norm_Black Voters`
  )
) +
  geom_hline(yintercept = 1.0, color="grey50") +
  geom_vline(xintercept = 1.0, color="grey50") +
  geom_abline(slope = -x_prop / y_prop, intercept = 1 + x_prop/y_prop, linetype="dashed") +
  annotate(
    "text",
    label = "Win Line", 
    x=0.05, y=1 +x_prop/y_prop, 
    angle= atan(-x_prop / y_prop) * 180 / pi
  ) +
  geom_text(
    aes(label = paste0(format_name(candidate)," ", year)),
    size=3.0
  ) +
  coord_fixed() +
  theme_sixtysix() +
  labs(
    title="Candidate performance in\n Black and White Moderate Divisions",
    x = "% of vote in White Moderate / Win Percent",
    y = "% of vote in Black Voter / Win Percent"
  )

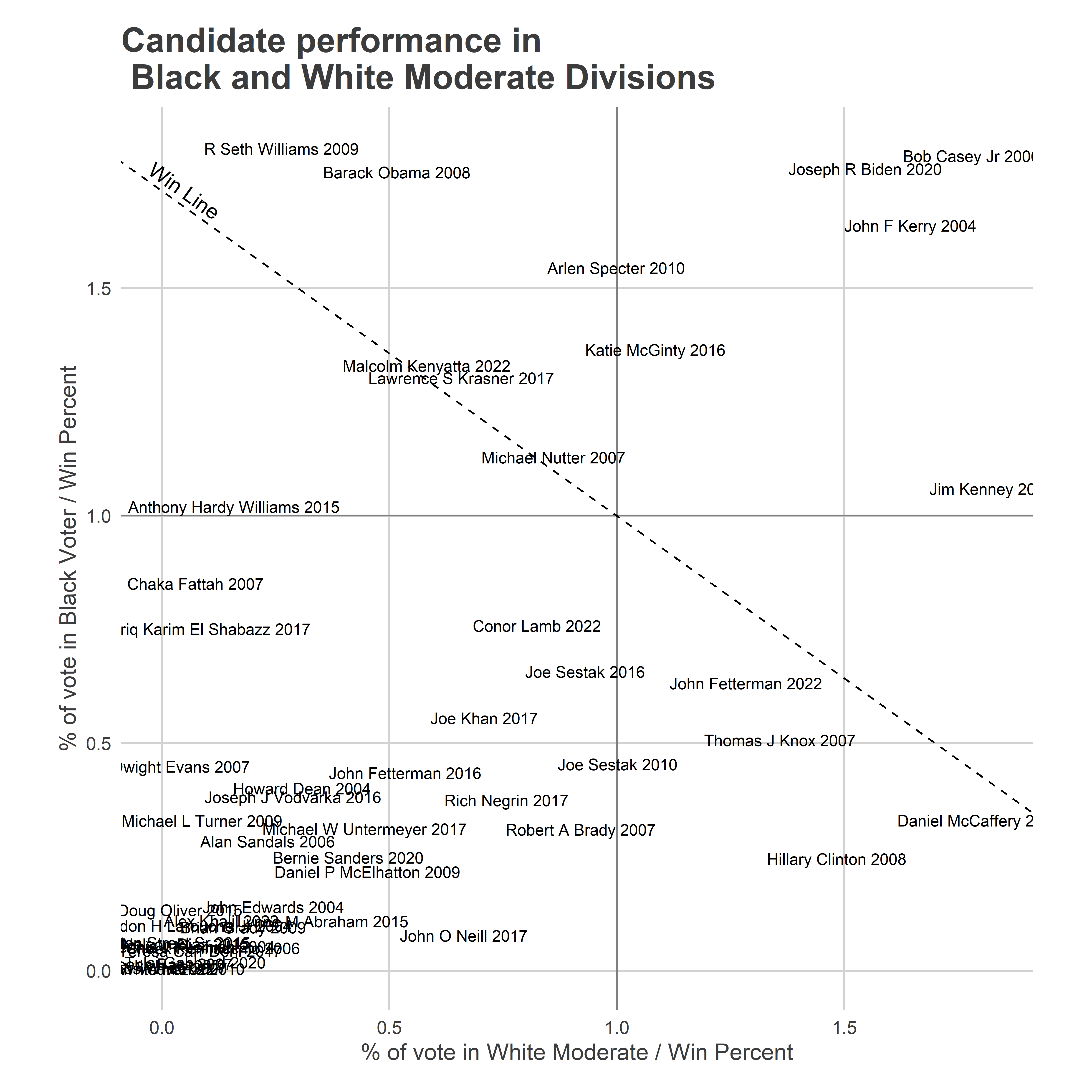
Seth Williams, Barack Obama, Arlen Specter, and even Katie McGinty did well enough in Black Voter divisions to overcome White Moderate weakness. Jim Kenney did much better in White Moderate divisions (although he still beat his win number in Black Voter divisions).

In all cases, an extremely strong showing in a bloc is 1.5 times the win number. This year, that would be 38%. Considering that, here are some combinations of candidates that would win. (To construct these, I’ve taken real candidates’ proportions in each bloc, and adjusted them proportionally up or down to hit exactly win number.)

View code 
profiles <- tribble(
  ~candidate, ~year, ~nickname,
  "BARACK OBAMA", "2008", "Black & Progressives",
  "MICHAEL NUTTER", "2007", "Progressive consolidator",
  "ROBERT A BRADY", "2007", "White Moderate consolidator",
  "JOSEPH R BIDEN", "2020", "Party stalwart",
  "ANTHONY HARDY WILLIAMS","2015", "Black consolidator",
  "JOE SESTAK", "2010", "White Moderates & Progressives"
)

profile_res <- cat_corr_df %>%
  inner_join(profiles) %>%
  mutate(candidate=case_when(
    candidate=="ROBERT A BRADY" ~ "BOB BRADY", 
    candidate=="JOSEPH R BIDEN" ~ "JOE BIDEN", 
    TRUE ~ candidate
  )) %>%
  mutate(total = 0.35 * `pvote_norm_Black Voters` + 0.3 * `pvote_norm_Wealthy Progressives` + 0.25 * `pvote_norm_White Moderates` + 0.1 * `pvote_norm_Hispanic Voters`) %>%
  mutate(
    across(
      `pvote_norm_Black Voters`:`pvote_norm_White Moderates`, 
      function(col) col / total * 0.25,
      .names="sim_{.col}"
    )
  ) %>%
  select(candidate, nickname, starts_with("sim_")) %>%
  pivot_longer(
    starts_with("sim_"),
    names_to = "cat",
    values_to = "pvote"
  ) %>%
  mutate(cat = gsub("sim_pvote_norm_", "", cat))

# win_types <- tribble(
#   ~name, ~`Black Voters`, ~`Wealthy Progressives`, ~`White Moderates`, ~`Hispanic Voters`,
#   "Black w enough Progressive", 0.38, 0.20, 0.20, 0.08,
#   "Progressive w some Black", 0.23, 0.38, 0.15, 0.18,
#   "White Moderate with Progressives", 0.08, 0.27, 0.45, 0.27
# ) %>%
#   mutate(
#     total = 0.35 * `Black Voters` + 0.3 * `Wealthy Progressives` + 0.25 * `White Moderates` + 0.1 * `Hispanic Voters`
#   )
# win_types

ggplot(
  profile_res,
  aes(x=cat, y=100*pvote)
) + 
  geom_hline(yintercept = 25, linetype="dashed") +
  geom_bar(aes(fill = cat), stat="identity") +
  scale_fill_manual(values = cat_colors, guide=FALSE) +
  geom_text(aes(label = sprintf("%0.0f", 100*pvote)), color="white", vjust = 1.4) +
  facet_wrap(~paste0(nickname, "\n(the \"", format_name(candidate), "\")")) +
  theme_sixtysix() %+replace%
  theme(axis.text.x = element_text(angle=45, hjust=1.1, vjust=1.1))+
  labs(
    title = "Possible Types of Winners",
    x=NULL,
    y="Percent of Vote to win"
  )

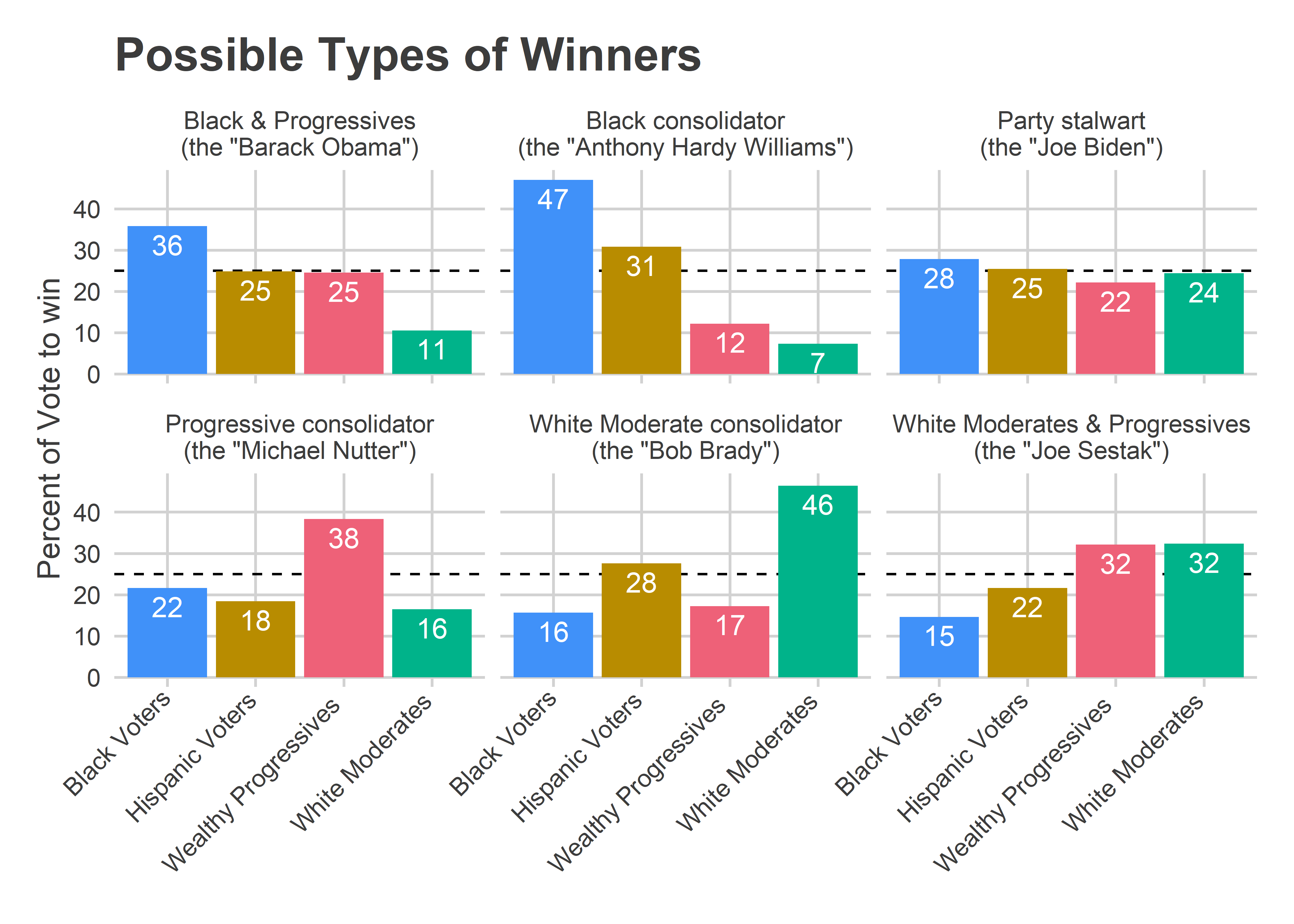
Notice that the single-bloc routes, the Anthony Hardy Williams and the Bob Brady, require herculean percentages in their bloc, nearly twice the 25% win number. More likely, the winner will do pretty well in both the Black Voter and Wealthy Progressive divisions, and manage to consolidate one of them.

Of course, how easy any of these paths are will depend on how many candidates are vying for them. Are too many candidates vying for the Black-, the Progressive-, or the White Moderate-lane? Coming in Part 2!

Posted on

Does ballot position matter for City Council?

This May, Philadelphia will be voting for City Council. This includes five city-wide Democratic At Large positions. We don’t yet know exactly how many At Large candidates there will be, but in 2019 there were 28 names on the ballot.

In order to arrange those names on the ballot, we famously draw names from a coffee can.

In the past, I’ve demonstrated that our judicial elections are determined by the random luck of drawing a good ballot position: being in the first column nearly triples your votes, and is more important than a Democratic City Committee endorsement and Philadelphia Bar Association Recommendation combined). I even proposed an NBA-wheel style ballot procedure that would fix the problem.

I’ve wondered if the same effect exists for City Council. There are reasons to expect not: voters pay more attention to City Council races and candidates spend more money, so it’s less likely that a voter will just push a button in the first column. But with voters choosing up to five names out of a pool of around 28 candidates, it’s certainly plausible they’ll take shortcuts.

I tried this analysis in January 2019 but didn’t have quite enough data. This time around I’ve added in 2019’s 28 candidates, and can finally measure some effects.

In 2019, all three incumbents plus Isaiah Thomas won handily. The fifth winner was Katherine Gilmore Richardson with 6.8% of the vote. Following her were Justin DiBerardinis with 6.3%, then Adrián Rivera-Reyes, Eryn Santamoor, and Erika Almirón at 5.3, 5.2, and 5.1% respectively.

View code 
library(tidyverse)
library(sf)

source("../../admin_scripts/util.R")


setwd("C:/Users/Jonathan Tannen/Dropbox/sixty_six/posts/council_ballot_position_23/")
df_major <- readRDS("../../data/processed_data/df_major_type_20220523.Rds")
ballot_position <- read.csv("../../data/processed_data/ballot_layout.csv")

Encoding(ballot_position$candidate) <- "latin1"
ballot_position$candidate <- gsub("\\s+", " ", ballot_position$candidate)

format_name <- function(x){
  x <- tolower(x)
  x <- gsub("(\\b)([a-z])", "\\1\\U\\2", x, perl=TRUE)
  x <- gsub("(á|ñ|ó)([A-Z]+)", "\\1\\L\\2", x, perl=TRUE)
  x <- gsub("\\s+", " ", x)
  x <- gsub("(^\\s)|(\\s$)", "", x)
  return(x)
}

council <- df_major %>% 
  filter(
    election_type == "primary",
      party == "DEMOCRATIC",
      office == "COUNCIL AT LARGE",
      year %in% c(2011, 2015, 2019)
  ) %>%
  mutate(year = as.integer(year))

council <- council %>% 
  left_join(ballot_position, by = c("year" = "year", "candidate" = "candidate"))

council$candidate <- factor(council$candidate)
levels(council$candidate) <- format_name(levels(council$candidate))
council <- council %>% filter(candidate != 'Write In')

council <- council %>%
  group_by(year) %>%
  mutate(ncand = length(unique(candidate)))

total_results <- council %>%
  group_by(candidate, year, row, column, ncand, incumbent) %>%
  summarise(votes = sum(votes)) %>%
  group_by(year) %>%
  mutate(
    pvote = votes/sum(votes),
    winner = rank(desc(votes)) <= 5
  )

YEAR <- 2019
ggplot(
  total_results %>% 
    filter(year == YEAR) %>% 
    mutate(
      lastname=format_name(gsub(".*\\s(\\S+)$", "\\1", candidate)),
      lastname=ifelse(lastname == "Jr",format_name(gsub(".*\\s(\\S+\\s\\S+)$", "\\1", candidate)),lastname),
    ) %>%
    arrange(votes),
  aes(y=row, x=column)
) +
  geom_tile(
    aes(fill=pvote*100, color=winner),
    size=2
  ) +
  geom_text(
    aes(
      label = ifelse(incumbent==1, "Incumbent", ""),
      x=column-0.45,
      y=row+0.45
    ),
    color="grey70",
    hjust=0, vjust=0
  ) +
  geom_text(
    aes(label = sprintf("%s\n%0.1f%%", lastname, 100*pvote)),
    color="black"
    # fontface="bold"
  ) +
  scale_y_reverse(NULL) +
  scale_x_continuous(NULL)+
  scale_fill_viridis_c(guide=FALSE) +
  scale_color_manual(values=c(`FALSE`=rgb(0,0,0,0), `TRUE`="yellow"), guide=FALSE) +
  expand_limits(x=3.5)+
  theme_sixtysix() %+replace% 
  theme(
    panel.grid.major=element_blank(),
    axis.text=element_blank()
  ) +
  ggtitle(
    paste(YEAR, "Council At Large Results"),
    "Democratic Primary, arranged by the ballot layout. Winners are outlined."
  )

Ballot position appears weaker than for judges: many candidates win from later columns. Incumbency is obviously the strongest factor.

But looking farther back, we see instances where ballot position appears to help. In 2015, Derek Green led the entire field as a challenger with the top position. And in 2011 Sherrie Cohen came in a close sixth place from the first column, and two more first column candidates were in the top nine.

View code 
ggplot(
  total_results,
  aes(y = 100 * pvote, color = interaction(incumbent, column==1))
) + 
  geom_text(
    aes(label = candidate),
    x=0, 
    hjust=0
  ) +
  facet_grid(. ~ year) +
  theme_sixtysix() +
  scale_y_continuous(breaks = seq(0,20,2.5)) +
  geom_text(
    data = tribble(
      ~votes, ~candidate, ~incumbent, ~year, ~pvote, ~column,
      # 1e3, "Challenger", 0, 2011, -0.007, 0,
      7e3, "Incumbent", 1, 2011, 0.007, 0,
      4e3, "First Column", 0, 2011, 0.000, 1
    ),
    fontface="bold",
    x=0.45,
    aes(label = candidate),
    hjust = 0,
    vjust=0
  ) +
  scale_color_manual(
    values=c(
      '1.FALSE' = strong_blue, 
      '1.TRUE' = strong_blue, 
      '0.FALSE'= "black", 
      '0.TRUE'=strong_green
    ),
    guide = FALSE
  ) +
  expand_limits(y=0) +
  labs(
    title="Incumbents Swept 2011 and 2019, but not 2015",
    y = "% of Vote"
  )

Let’s use regression to tease apart the effects. I’ll regress the percent of the vote received by a candidate on being in the first column and being in the first row, incumbency, and year fixed effects. The regression is simplistic, but since ballot position is randomized we don’t need anything more. (The substantive findings below are robust to more controls and to using log(votes).)

View code 
ols_fit <- lm(
  100 * pvote ~ 
    as.character(year) +
    incumbent +
    (row == 1) +
    (column == 1) + 
    # (column == 1 & row == 1) +
    # (column == 1 & row != 1) +
    # (column == 2) +
    1,
  data = total_results #%>% filter(!incumbent)
)
# summary(ols_fit)

print_coef <- function(fit, coef){
  val <- round(ols_fit$coefficients[coef], 1)
  se <- summary(ols_fit)$coefficients[,2][coef]
  # stars <- case_when(p<0.01 ~ " (p < 0.01)", p < 0.05 ~ " (p < 0.05)", TRUE ~ "")
  se_text <- paste0(" (",round(se, 1),")")
  prefix <- (if(val > 0) "+" else "")
  paste0(prefix, val, se_text)
}

tribble(
  ~Effect, ~"% Vote in pp (standard error)",
  "Baseline Votes 2019", "2.6",
  "Incumbency", ols_fit %>% print_coef('incumbent'),
  "First Column",  ols_fit %>% print_coef('column == 1TRUE'),
  "First Row",  ols_fit %>% print_coef('row == 1TRUE')
) %>% 
  knitr::kable("html") %>% 
  kableExtra::kable_styling(full_width = F)
Effect % Vote in pp (standard error)
Baseline Votes 2019 2.6
Incumbency +6.4 (0.9)
First Column +2.4 (0.9)
First Row -0.3 (0.8)

Non-incumbent candidates in the second or later column started with an average 2.4% of the vote in 2019. Incumbents on average receive 6.4 percentage points more votes. Candidates in the first column receive on average 2.4 pp more votes. Being in the first row doesn’t appear to help.

So the first-column effect for City Council is smaller than for Common Pleas, but still nearly doubles a typical challenger’s votes. And in 2019 it would have been enough to put any of the close challengers (Gilmore Richardson, DiBerardinis, Santamoor, Almirón) over the top.