Posted on

Why Bullet Voting is probably a bad idea

The answer: Combinatorics.

Different kind of post today. Time for some game theory (or just math? I dunno.)

Commissioner Schmidt tweeted this on Tuesday.

It references Bullet Voting, a topic his Office has covered in great detail before. Bullet voting is the act of voting for a single candidate even when you’re allowed to vote for more. A lot of voters do it, either because they think it gives their favorite candidate a better chance to win, or as a cathartic experience. According to another infographic, 19% of Democrats voted for a single At Large candidate on May 21st.

Today, I argue that Bullet Voting is almost always sub-optimal. To make Bullet Voting the right decision, you don’t just need to have a candidate that you love, but a candidate that you love many times more than your second favorite candidates, because you’re hurting your foregone candidates in many more scenarios than you’re helping your favorite one.

Let’s do some math.

Three-Candidate Example

First, consider a simple race.

Suppose there are three candidates for two positions: A , B , and C . A is your favorite, B your second favorite, and C your least.

Write the value you get from two candidates winning as V(A,B) (if e.g. A and B won). Let’s make a simplifying assumption that

V(A,B)=V(A)+V(B) ,

that is, the value of winners is independent of each other, is additive, and the order of their win doesn’t matter. This doesn’t seem too restrictive, but it does mean you don’t have either (a) teams of candidates who are better together than separate, or (b) diminishing returns to candidates, so having two A s really would be twice as good as having one.

The question: Should you vote for both A and B, or bullet vote for A? Assume that in the case of a tie, a coin is flipped for the winner. (I’ll ignore three-way ties).

It helps to frame it as the following: suppose everyone else in the city has voted. You don’t know what the results are, but it’s done. Your choice of bullet voting for A instead of voting for A and B could have the following effects, and only the following effects:

  • It could win the election for A if A is losing to B by 1 vote or tied.
  • It could lose the election for B if B is losing to C by 1 vote or tied.

That’s it. Bullet voting helps your favorite candidate beat your second tier candidate, but your foregone vote harms your second tier candidate against the third. Importantly, notice that it has no effect on whether A beats C, head-to-head.

This means the expected benefit from bullet voting is

0.5 (V(A)−V(B)) p(C, B>A) − 0.5 (V(B)−V(C)) p(A,C>B)

where the notation p(C, B>A) is the probability that among everyone else’s votes, C is in first, and A is either tied with or one vote behind B . (The 0.5 comes from the coin flip. If there is a 4% chance that A ties B, A would still win half of those, so your vote only increases A‘s win probability by 2%). To interpret the equation above, bullet voting for A increases your value by the value-add of A over B if A is losing to B by one vote, but costs you the value of B over C if B is losing to C by one vote. The choice has no effect in any other ordering. Let’s drop the 0.5, since that multiplies everything, and call the marginal value of the bullet vote:

Marginal Value of Bullet Vote = (V(A)−V(B)) p(C,B>A) − (V(B)−V(C)) p(A,C>B).

You should bullet vote whenever this value is positive.

Consider some cases. (1) If all candidates have equal chances of winning, so that p(C,B>A)=p(A,C>B), then you should bullet vote when V(A)−V(B) > V(B)−V(C), i.e. when the gap in value between A and B is larger than the gap in value between B and C. If you have a strong preference for A, but B and C are interchangeable, then bullet vote for A. But if what really matters is keeping C out of office, then vote for A and B.

(2) If C is a runaway winner, so that p(C,B>A) is much larger than p(A,C>B), then you should bullet vote for A; it’s basically a two-person race.

With more candidates, bullet voting becomes less appealing.

Now, suppose candidate D joins the race. D is somehow even less preferable than C. We will still only have two winners.

Bullet voting for A still only makes a positive difference in the case where A is losing to B by one vote or tied, but foregoing voting for B now hurts you when B is losing to C *or* D by one vote or tied.

In this case, the marginal value of bullet voting is

E[V|Bullet vote for A]−E[V|Vote for both A and B]=
(V(A) − V(B)) (p(C, B>A, D) + p(D, B>A, C))
−(V(B) − V(C)) (p(A, C>B, D) + p(D, C>B, A))
−(V(B) − V(D)) (p(A, D>B, C) + p(C, D>B, A))

This is messy, but it’s basically the difference in value between A and B times the probability that your vote would prove decisive in A beating B, minus the differences in value between B and C, and B and D, times the probabilities your vote would be decisive there. Notice that we don’t need to include cases where A loses to C or D by one vote; your decision to bullet vote or not doesn’t change those head-to-head matchups.

Notice that the value math has completely changed. Now, if all the orderings of candidates are equally probable, the value-add of A over B would need to be twice as large as the value-add of B over C/D because your additional vote for B is decisive in twice as many scenarios as your bullet vote for A . This is the key: the power of the combinatorics means that bullet voting harms your second-favorite candidates in many times more scenarios than it helps your favorite one. And this is why bullet voting is usually a bad idea; it only makes sense if the value-add of your preferred candidate versus your second favorites is many times larger than the value-add of your second favorites versus the rest.

Consider some numbers. Suppose you think candidate A gives you a value of 10, B a value of 4, and C and D are worthless at 0. (The value can represent anything: good to the world, improvement to your life. Whatever you optimize for.) And suppose you think all candidates have equal chances of winning. Should you bullet vote for the candidate you love, A? No. That only helps in the case where A is losing to B by one vote among everyone else, in which case it gives you +6 value. But your foregone vote for B costs you -4 if they lose to C or D, and that is twice as likely to happen: when B loses by a vote to C, and when B loses by a vote to D.

5 slots, 10 candidates

Now let’s consider a situation close to the City Council race on May 21st. Suppose there is a single candidate, A, you love. There are four candidates, B, C, D, and E, who are good. There are five candidates, F, G, H, I, and J, that you dislike. The race actually had more candidates, but suppose only these ten had plausible chances. Let’s further assume that among these candidates, all possible election orderings are equally possible.

Bullet voting for A helps you when B, C, D, or E are beating A by one vote. But it hurts you when any of B, C, D, or E are losing to any of F, G, H, I, or J. Thats 4 scenarios where it helps, but 20 scenarios where it hurts you. Bullet Voting only makes sense if the average gap in your preferences for A vs B/C/D/E is five times larger than the average gap in your preferences for B/C/D/E vs F/G/H/I/J.

You can complicate this by giving each ordering of candidates different probabilities of occuring, but the math of the combinatorics will probably swamp whatever you come up with: the chances that one of your second tier candidates is losing to a third tier candidate will almost always be many times greater than the probability your favorite candidate is losing to a second tier candidate. And Bullet Voting only helps in that second scenario. It only makes sense to bullet vote if the gaps in your preferences are equally disproportionate in the opposite direction.

Note: While I think it’s unlikely that the gap between candidates A and B is five times larger than the gap between B and F, it certainly isn’t impossible. I definitely knew voters in the Primary for whom the value of their personal favorite candidate was five times larger than the gap between their second favorite and sixth; for them, bullet voting was optimal. But it comes at a steep cost.

General Solution

More generally, suppose you are able to vote for K out of C candidates. You have a single favorite candidate, K−1 second favorites, and C−K left over candidates. Let them be ordered, and indexed by i, so i=1 is your favorite and i=C your least favorite. If you bullet vote, you decrease the likelihood that your favorite loses to your second favorites, at the cost of increasing the chances that your second favorites lose to the leftovers.

The value of the Bullet Vote, versus voting for all K, is

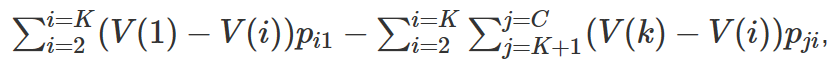
where $p_{ji}$ is the probability that among all voters but yourself, candidate j is in Kth place and is tied with i or beating them by a single vote (it’s all of the combinations of P(A>B>…) from above.) I’ve again divided everything by 0.5 for simplicity. Notice that the first summation has K−1 terms, while the second has (K−1)(C−K) terms. If the probabilities are all equal, the average difference in values in the first sum must be C−K times larger than the average difference in values in the second sum for bullet voting to be optimal.

The exact solution for a given race will depend on (a) the gap between your preferred candidate and the others you would vote for, (b) the gap between those others and the candidates you don’t want to win, and (c) the relative probabilities of everyone winning. But the combinatorics will be salient in every scenario.

Example: Third Party Voting

In November’s City Council election, there will be five Democrats, five Republicans, and a number of third party candidates on the ballot for seven At Large spots. Voters can vote for up to five candidates, and the Philadelphia Charter stipulates that no more than five winners can come from the same party. This usually means the five Democrats win in a landslide, and two of the Republicans win. Suppose you wanted to minimize the chance that a Republican would win a seat. What would be the optimal strategy?

Finding one: Bullet Voting doesn’t help. Voters might think Bullet Voting for two third party candidates helps them more than voting for three Democrats and two third party candidates. This isn’t right. Remember that bullet voting only help the candidates you do vote for against the candidates you would have voted for. Here, bullet voting would help the third party candidates if they came within one vote of the Democrat you would vote for. They have the same chance of beating the Republican if you spend a vote on the Democrats or not.

Finding two: Voting for Democrats is also wrong. If you think there is a 100% chance that all the Democrats will win (which there is), then notice that all of their pp s in the sums above are zero: there is no chance that they happen to lose to someone else by a single vote. Thus, it doesn’t help to vote for them.

So it doesn’t help to bullet vote, but it also isn’t optimal to vote for Democrats. What should you do? The best way to beat all the Republicans is to spend all of your votes on third party candidates; this eliminates the chance that you happen to bank on the wrong one, with no effect on the Democrats who are guaranteed to win. If there aren’t enough third party candidates to spend all five of your votes on, you can spend one on your favorite Democrat; it doesn’t make a difference either way (see above).

(Of course, this assumes that you do prefer each of the third party candidates to the Republicans. If you prefer a Republican to a third party candidate, you would have to work out all the summations above to decide if you should vote for that Republican or just withhold a vote.)

So, should you Bullet Vote?

Probably not.

Posted on

A note on names

I’ve received some good feedback about the names I used in my analysis of Philadelphia’s voting blocs. In that piece, I divided Philadelphia’s divisions into four groups that all voted similarly. Today, I’m taking a moment to walk through the method, the naming process, and then lay out some changes I’ll make moving forward.

Where the dimensions come from

To figure out Philadelphia’s dimensions, I used historic election results. I used Singular Vector Decomposition to ask, “In what divisions do candidates do similarly well?” Importantly for this discussion, the method uses only voting data; I didn’t input any demographic or neighborhood information. I just asked of the data: if a candidate did well in Division X, what other divisions did they do well in?

Here are the four clusters that produced:

When the method produces the dimensions, it doesn’t provide any names, or any other clues as to why the divisions might be similar. It just says “over the last 17 years, candidates who did well in one red divisions tended to do well in the other ones”. Adding names (in an attempt to make my analysis readable) was entirely done by me, after the fact.

Choosing names

So, here’s where I sat. I saw these groups, and needed to figure out the unifying element. The first cluster that I named was the red one that unites Center City and the ring around it with Chestnut Hill and much of Mount Airy. I called these the “Wealthy” divisions. These are the parts of the city with the highest median incomes and highest home prices.

The name was a little blunt, but honestly, I liked that about it: Philadelphia is the eleventh-most segregated metropolitan region in the US (self-cite), and using a euphamism to bury the fact that wealth was the thing these divisions all had in common would only serve to make people who live in these segregated communities (including me) feel better about themselves. I like to use clear, non-euphamistic names that illustrate the way by which the groups were defined, and “Wealthy” is the obvious best word for these divisions.

The next clusters I named were blue and orange. These clusters overlap in incomes, but blue covers Point Breeze, Southwest, West, North, and parts of Northwest Philadelphia, while orange unites the Northeast and River Wards with deep South Philly and Manayunk. Again, the decisive factor isn’t subtle: the blue divisions are almost entirely predominantly Black, and the orange divisions predominantly White.

I couldn’t just call these by the racial demographics, though, because I already had a cluster whose name didn’t depend on race, “Wealthy”. I was worried that having one cluster named “Wealthy” and another “Black” would semantically imply that wealth was mutually distinct from Blackness. So I decided to call them “Black non-wealthy” and “White non-wealthy”, which would safely acknowledge that divisions in the Wealthy cluster could be both White or Black. I was in the clear.

Of course, that’s not really how folks read it. Instead, it felt like I was making a statement about the wealth of the residents. I think there were two features of the names that made people uncomfortable, one that I’m ok with, and one that I want to change.

First, what I want to change: It was a problem that I used a negation in the names–“non-Wealthy” instead of “Moderate Income” or “Working Class”. The first focuses on a comparison with someone else, while the second considers the given divisions without any comparison. That values what they are, without focusing on what they’re not. It’s similar to how people blanche when you call yourself an atheist, but are generally cool with you calling yourself a humanist; one focuses on what you’re not, and feels like a challenge, the other focuses on what you are.

I haven’t found the exact term for these clusters that I love yet. Both “Moderate Income” and “Working Class” feel either ill-defined or euphamistic, but I’ll keep thinking (suggestions welcome!). But I definitely won’t be using “non-wealthy” any more.

The second reason I think the names bothered people is the broad way they lumped together divisions. The blue cluster combines a diverse set of neighborhoods, from West Philly, to North Philly, up to West Oak Lane. While it’s true that all of the divisions are predominantly Black, the neighborhoods are different in other ways, and residents are rightfully wary of all being lumped together and treated as a monolithic group.

This is the concern that I think I’m ok with. While these divisions are different in myriad ways, it turns out that they all typically vote for the same candidates. If we were studying something else, we would want categories that handled those differences. But in studying voting patterns, grouping together these divisions is useful.

One important thing: I don’t know the causality of why these places all vote similarly. Obviously the racial similarity is important, but I don’t know if the specific causal mechanism is that the wards endorse similar candidates, or if residents have similar preferences, or if candidates target their outreach to the same neighborhoods. That’s obviously a crucial question, but it’s not one I’ve figured out how to disentangle yet.

Moving forward

So that’s where I’m at. I won’t go back and change the posts that I’ve already written. That would gloss over this useful discussion. But I’ve added a note there, and I’ll come up with better names before I use the clusters again.

The inspiration for this post was some great conversations with readers. I love hearing from you! I’m still surprised that people are reading, and more surprised when folks wanna engage. jonathan dot tannen at gmail dot com.

Update 2019-06-30: The names I’ve chosen

I’ve settled on names. After a lot indecision, I had a stroke of insight that is obvious in retrospect: if I use only voting patterns to identify the clusters, I should name them based on those voting patterns. This is the necessary response to my claim above that I should choose dimension names close to the definitional aspect of the clusters. So here are my chosen names:

  1. Black Voters
  2. Wealthy Progressives
  3. White Moderates
  4. Hispanic North Philly

These feel right to me. The main difference between the Center City divisions and Northeast/South Philly is between support for progressive vs centrist candidates (think Krasner vs Khan/O’Neill). The Black divisions don’t obviously line up along that dimension, supporting Krasner in 2017, but not the Wealthy Progressive favorites of DiBerardinis and Almirón. When these divisions differ, it is often to support Black candidates. The Hispanic divisions form a largely contiguous block of North Philly, allowing me to attach the neighborhood name to it.

These names manage to be clear, and enunciate the differences between the clusters without euphamism. But they also don’t editorialize, and stay faithful to how the divisions vote differently. So these are what I’ll use. Until I change my mind again.