How did the Common Pleas judges win?

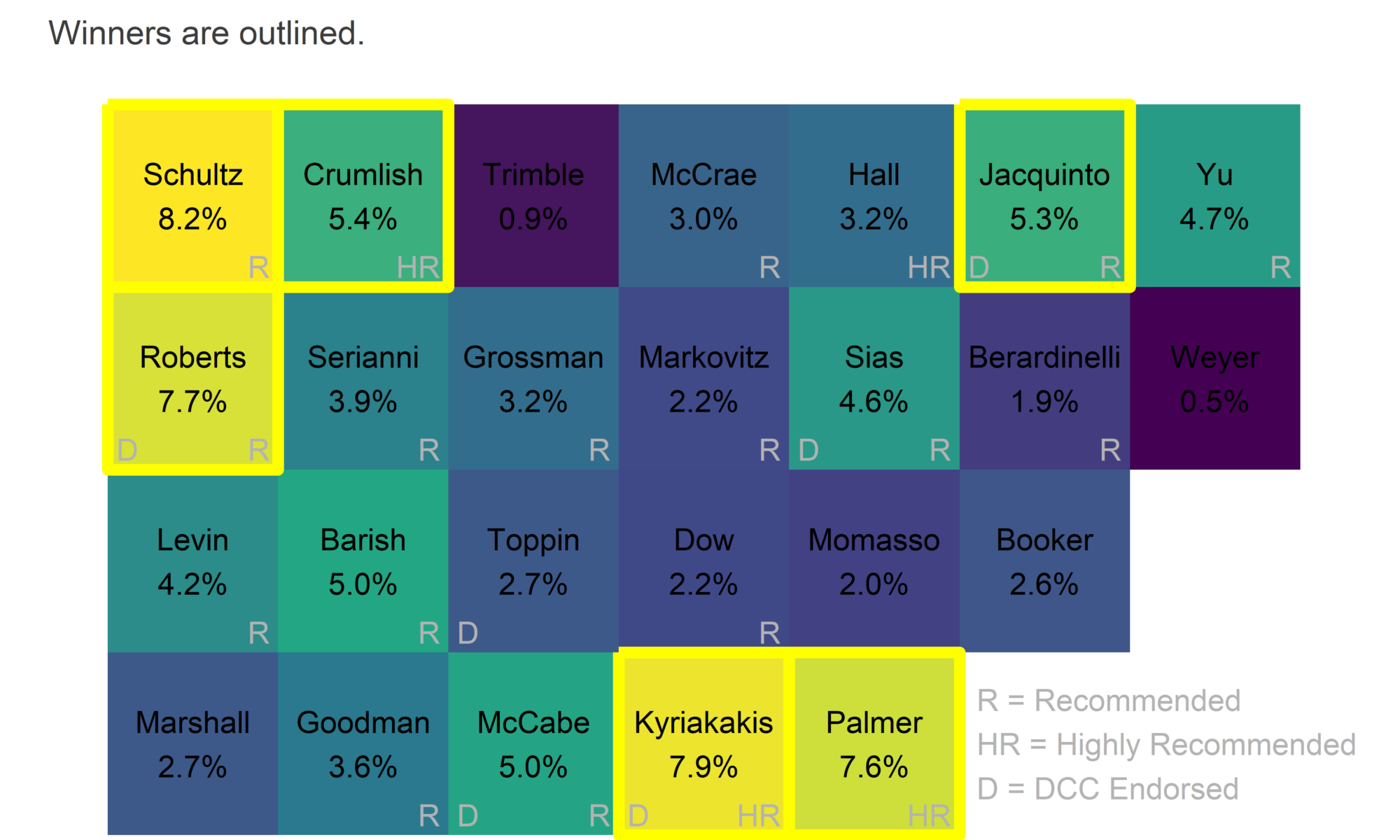
Ahead of May 21st, I made some predictions about the Court of Common Pleas. I predicted a 66% chance that all six winners would be Recommended by the Bar; they all were. I predicted that 2.5 candidates would win from the first column and 1.0 from the second; those columns produced 2 and 1 winners, respectively.

But I’m here today to talk about something I got very, very wrong. Here’s something I wrote:

We get no Highly Recommended winners in 46% of simulations, and only one in another 47%. […] Getting two [Highly Recommended] winners (let alone three or four) would be a huge achievement, and presumably good for the citizens of Philadelphia, too.

Well, three Highly Recommended candidates won. I was pretty sure that wouldn’t happen, I gave it a 7% chance. To be fair, things with 7% chances happen all the time, but I actually think something changed this election. The Bar’s High Recommendations flexed their muscle.

Who won, and where

Looking at the layout of the ballot, you can tell yourself an easy story about how most candidates won.

View code

library(tidyverse)
df <- read_delim(
  paste0("../election_night_needle/raw_data/PRECINCT_2019525_H08_M09_S54.txt"),
  delim = "@"
) %>%
  rename(
    OFFICE = `Office_Prop Name`,
    candidate = Tape_Text,
    warddiv = Precinct_Name
  )

df <- df[-(nrow(df) - 0:1),]

df <- df %>% group_by(warddiv) %>%
  filter(sum(Vote_Count) > 0) %>%
  group_by()

df_cp <- df %>% filter(OFFICE == "JUDGE OF THE COURT OF COMMON PLEAS-DEM")

View code

format_name <- function(x){
  x <- tolower(x)
  x <- gsub("\\b([a-z])([a-z]*)", "\\U\\1\\L\\2", x, perl=TRUE)
  x <- gsub("\\bMc([a-z])", "Mc\\U\\1", x, perl=TRUE)
  return(x)
}

ballot <- read_csv("../../data/common_pleas/judicial_ballot_position.csv") %>%
  mutate(lastname = gsub(".* ([A-Za-z]+)$", "\\1", name) %>% format_name())

df_cp <-  df_cp %>%
  filter(candidate != "Write In") %>%
  mutate(
    candidate = format_name(candidate),
    Last_Name=format_name(Last_Name), 
    First_Name=format_name(First_Name)
  )

ballot <- ballot %>%
  filter(year == 2019) %>%
  left_join(
    df_cp %>% select(candidate, Last_Name) %>% unique, 
    by = c("lastname" = "Last_Name")
  )

cp_overall <- df_cp %>%
  group_by(Last_Name, First_Name) %>%
  summarise(VOTES = sum(Vote_Count)) %>%
  group_by() %>%
  mutate(
    winner=rank(desc(VOTES)) <= 6,
    pvote = VOTES / sum(VOTES),
    lastname=Last_Name
  ) 
  
cp_overall <- cp_overall %>% left_join(ballot %>% filter(year == 2019))

ggplot(
  cp_overall %>% arrange(VOTES),
  aes(y=rownumber, x=colnumber)
) +
  geom_tile(
    aes(fill=pvote*100, color=winner),
    size=2
  ) +
  geom_text(
    aes(
      label = ifelse(philacommrec==1, "R", ifelse(philacommrec==2,"HR","")),
      x=colnumber+0.45,
      y=rownumber+0.45
    ),
    color="grey70",
    hjust=1, vjust=0
  ) +
  geom_text(
    aes(
      label = ifelse(dcc==1, "D", ""),
      x=colnumber-0.45,
      y=rownumber+0.45
    ),
    color="grey70",
    hjust=0, vjust=0
  ) +
  geom_text(
    aes(label = sprintf("%s\n%0.1f%%", lastname, 100*pvote)),
    color="black"
    # fontface="bold"
  ) +
  scale_y_reverse(NULL) +
  scale_x_continuous(NULL)+
  scale_fill_viridis_c(guide=FALSE) +
  scale_color_manual(values=c(`FALSE`=NA, `TRUE`="yellow"), guide=FALSE) +
  annotate(
    "text",
    label="R = Recommended\nHR = Highly Recommended\nD = DCC Endorsed",
    x = 5.6,
    y = 4,
    hjust=0,
    color="grey70"
  ) +
  theme_sixtysix() %+replace% 
  theme(
    panel.grid.major=element_blank(),
    axis.text=element_blank()
  ) +
  ggtitle(
    "2019 Common Pleas Results",
    "Winners are outlined."
  )

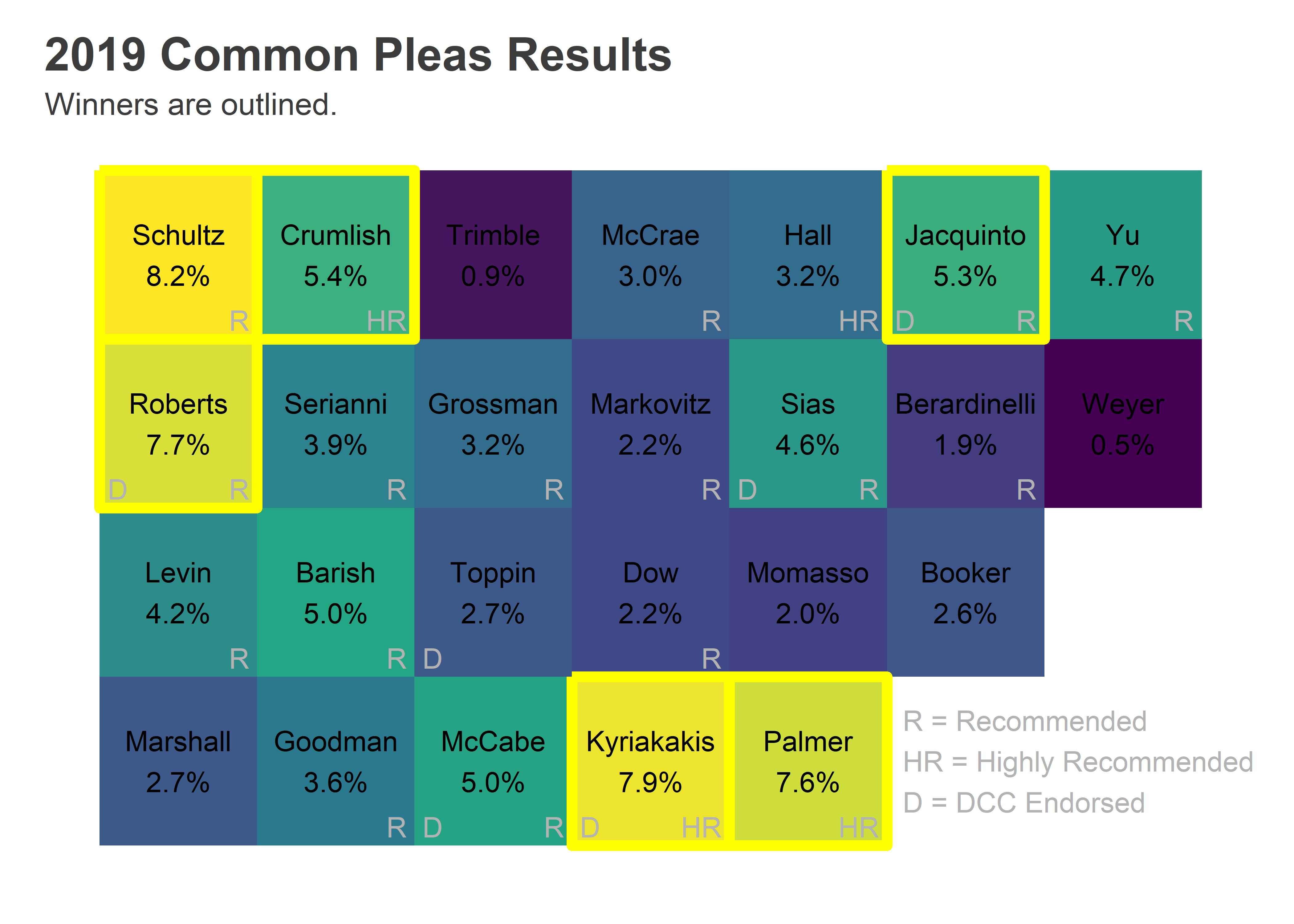
Jennifer Schultz won with number one ballot position and a Bar Recommendation. Joshua Roberts combined the first column with a Bar Rec and a Democratic City Committee endorsement. Crumlish had the top of the second column plus a High Recommendation. Kyriakakis and Jacquinto combined Bar Recommendations with DCC endorsements.

The person who my model thought absolutely, positively would not win was Tiffany Palmer. And she romped by 2.6 points.

When I published my predictions, I didn’t share the candidate-level results. That’s because my model only used structural factors, and knew nothing about candidates themselves. It would perform well at overall counts, while looking pretty silly for individual candidates. It knew, for example, that some candidates would be breakaway stars from the third column or later, but spread that probability among all of them.

Well, let’s go back and look under the hood at the candidate predictions themselves.

View code

cp_sim <- read.csv("../simulating_cp/simdf.csv")
cp_overall <- cp_overall %>% left_join(cp_sim %>% mutate(name=format_name(name)))

cp_overall <- cp_overall %>% arrange(desc(mean_pvote)) %>%
  mutate(name=factor(name, levels=name))

ggplot(
  cp_overall,
  aes(x=name, y=100*mean_pvote)
) +
  geom_point() +
  geom_errorbar(
    aes(ymin=100*pvote_05, ymax=100*pvote_95),
    width=0
  ) +
  geom_point(aes(y=100*pvote), color=strong_purple, size=2) +
  theme_sixtysix() %+replace%
  theme(axis.text.x = element_text(angle=-90, hjust=0)) +
  scale_x_discrete(NULL) +
  scale_y_continuous("Percent of Vote") +
  expand_limits(y=0) +
  ggtitle("Simulated and actual Common Pleas results") +
  annotate("point", x = 15, y = 12, size=2, color=strong_purple) +
  annotate("text", x = 15.4, y = 12, size=4, color=strong_purple, hjust=0, label="Actual Results", fontface="bold") +
  annotate("point", x = 15, y = 14) +
  annotate("errorbar", x = 15, ymin = 13.5, ymax=14.5, width=0) +
  annotate("text", x = 15.4, y = 14, size=4, hjust=0, label="Simulated 90% Credible Interval", fontface="bold")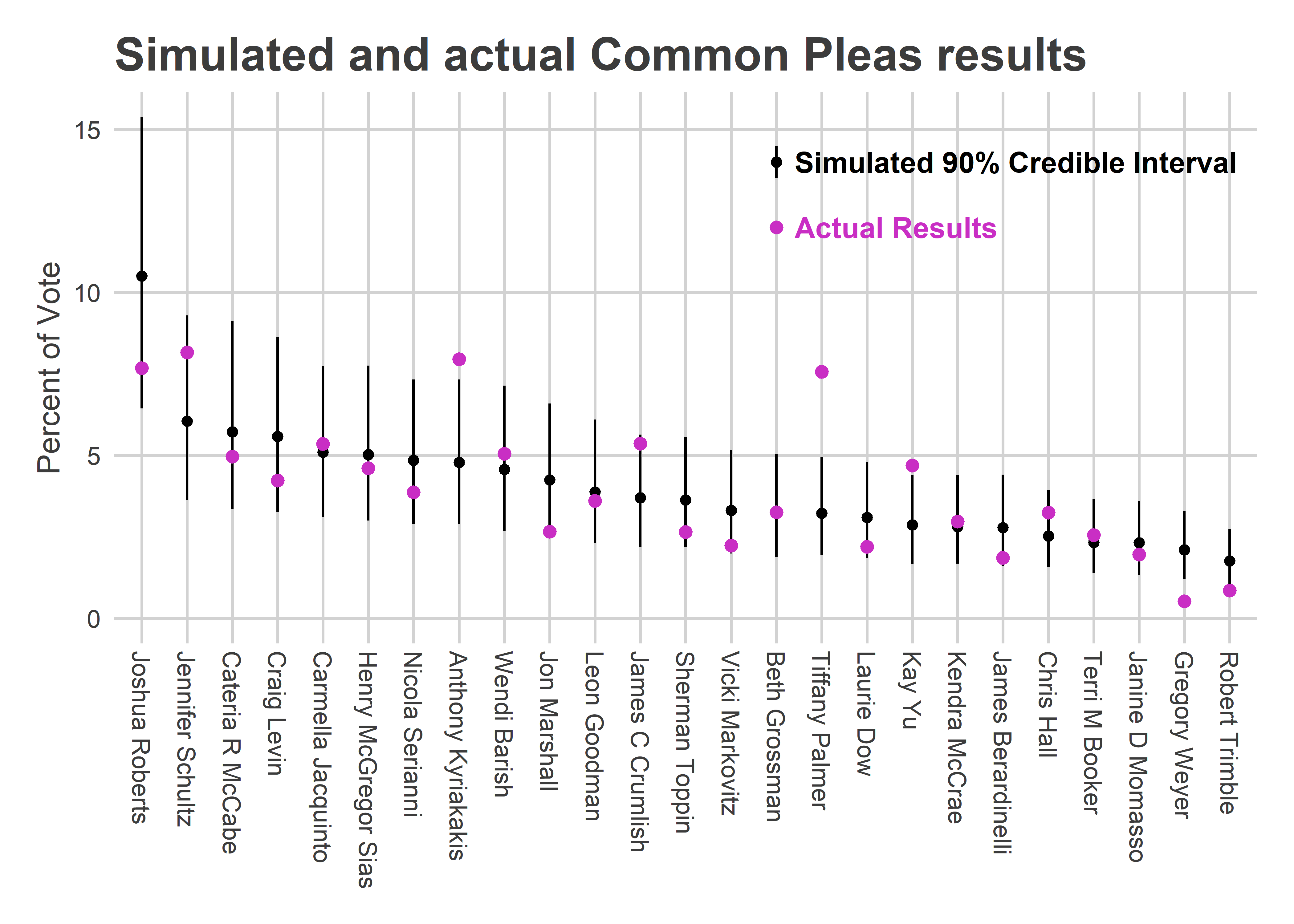

Kyriakakis and Palmer greatly exceeded the 90% credible range, and James Crumlish was at the top of it. Those three Highly Recommended candidates were all in the top four candidates who most overperformed my prediction (Kay Yu was the other).

I significantly underestimated the Highly Recommended candidates this time. But it wasn’t my fault! Two years ago, the Bar didn’t Highly Recommend anybody. Four years ago, they Highly Recommended three; they all won, but didn’t appear to receive any more votes given their ballot position than the regular Recommendeds. So it was reasonable coming into this election to think that High Recommendations were just like regular ones.

The map of the winners’ votes makes it even clearer how each won.

View code

library(sf)
divs <- st_read("../../data/gis/2019/Political_Divisions.shp", quiet=TRUE) %>%
  mutate(warddiv=paste0(substr(DIVISION_N, 1, 2), "-", substr(DIVISION_N, 3, 4)))

df_cp <- df_cp %>% 
  group_by(warddiv) %>% 
  mutate(pvote = Vote_Count/sum(Vote_Count)) %>%
  left_join(cp_overall, by=c("candidate"), suffix=c("",".y")) %>%
  group_by()
div_cp <- divs %>% 
  left_join(df_cp)

winners <-cp_overall %>% arrange(desc(pvote)) %>% with(candidate[1:6])

ggplot(
  div_cp %>% 
    filter(candidate %in% winners) %>% 
    mutate(candidate = factor(candidate, levels=winners))
) +
  geom_sf(aes(fill=pmin(100*pvote, 18)), color=NA) +
  facet_wrap(~candidate)+
  theme_map_sixtysix() %+replace% theme(legend.position = "right") +
  scale_fill_viridis_c(
    "Percent of Vote", 
    labels=function(x) paste0(x, "%", ifelse(x>=18,"+",""))
  ) +
  ggtitle("Common Pleas winners' results")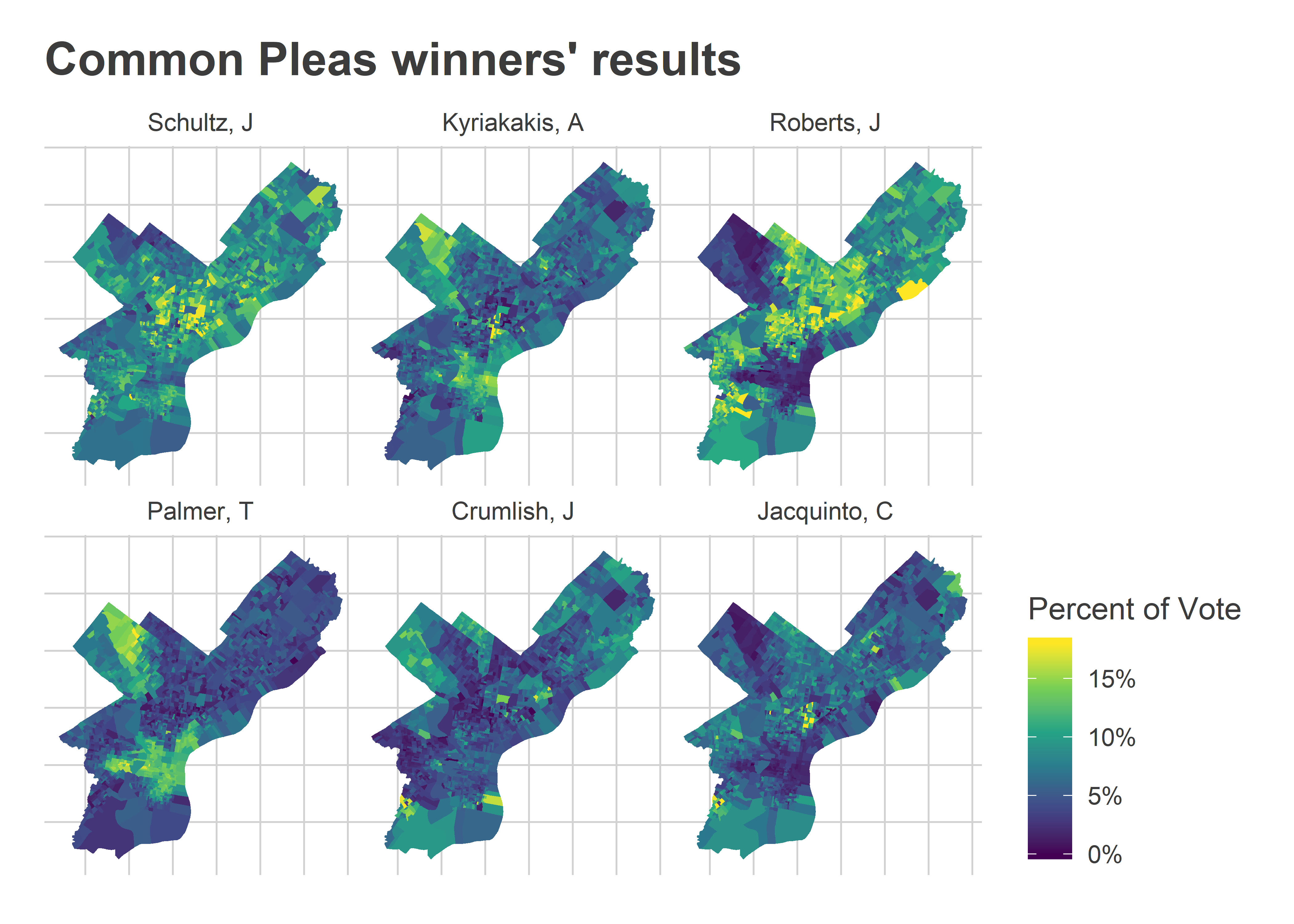

Schultz won across the board: a telltale sign of the top ballot position. Roberts and Jacquinto won on the back of the DCC endorsements (with Roberts’s votes being super-charged by the second ballot position).

Crumlish did oddly well in the 50th and 10th wards in the Northwest (that nub of green at the top center). Those wards have powerful endorsements, and he wasn’t DCC endorsed. But it turns out he was in fact endorsed there. Here’s an image submitted to Max Marin’s #phillyballots collection:

View code

knitr::include_graphics("ward_50_endorsements.jpg_large")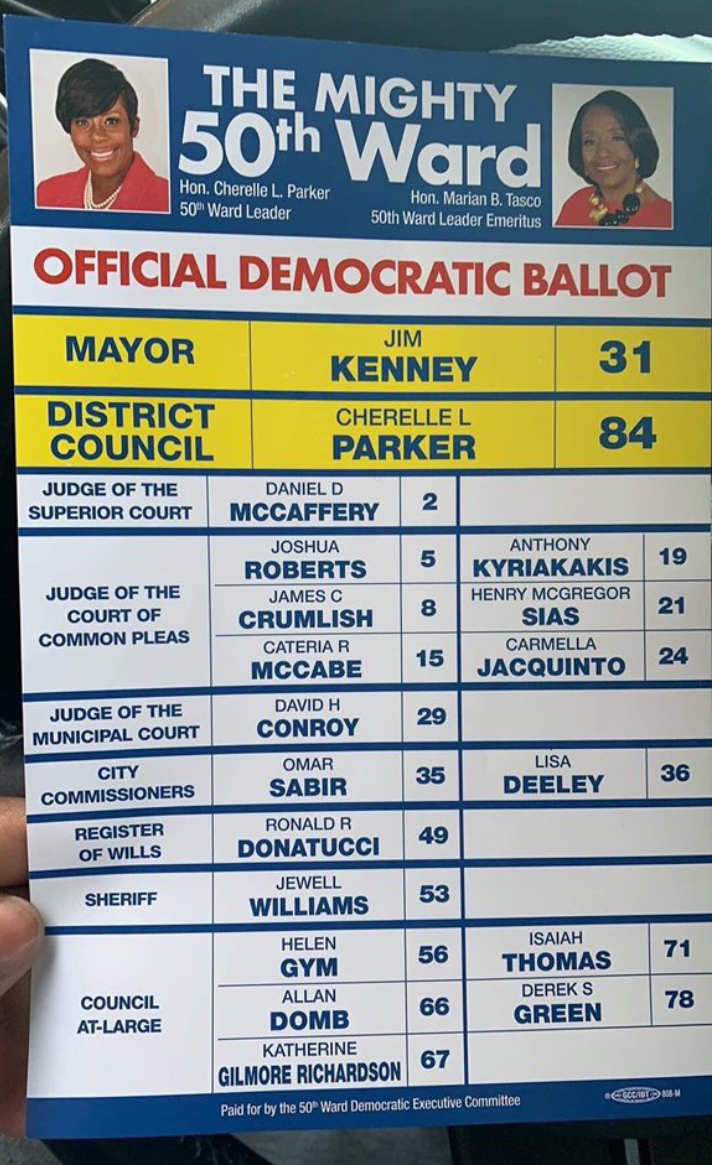

Kyriakakis and Palmer won with the wealthier wards (Center City and its ring, and Mount Airy/Chestnut Hill). This is where we’d expect the Bar Association’s Recommendations to matter most.

Have we done away with unqualified judges? Probably not.

All six of our winners were Recommended by the bar. This is a big improvement from the last two elections, which had three Not Recommended winners each.

But largely, that was luck. There was only one Not Recommended candidate in the first two columns of the of the ballot. Looking at the scatterplot above, the election went basically as predicted, except for the Highly Recommended dominance of Kyriakakis and Palmer. But nothing else has changed; especially the fact that a Not Recommended candidate at the top of the first ballot would probably have won.

How did the Highly Recommended Candidates win?

There are three reasons Highly Recommended candidates might have romped:

The High Recommendations themselves directly cause the win.
The High Recommendations made other causes easier to get (money, ward endorsements, buzz). These are called “mediators”.
The High Recommendations were in response to other traits of the candidates, and they would have won anyway. We call this “selection” or “omitted variable bias”.

Let’s lay out some evidence for each (out of order).

First, the evidence for mediating factors. Notice that having a High Recommendation was not sufficient for overperforming. Kyriakakis and Palmer did overperform, but Crumlish and Hall didn’t. That also matches with the timing of the High Recommendations: Kyriakakis and Palmer got theirs early on, Palmer and Hall much later. [The Bar recommendations come in on a rolling basis, depending on when the candidate submits their application and the timing of the investigative committee.]

This suggests to me that Kyriakakis and Palmer had time to milk that recommendation for other endorsements and to gain momentum in fundraising to spend on wealthy-neighborhood advertising. The mechanism was not, as a counterexample, just people looking up who was Highly Recommended. Otherwise Hall and Crumlish would have done better.

Second, it may have been that the High Recommendation just responded to factors that would have made Kyriakakis and Palmer do better anyway. Here are the results for Kay Yu, who also overperformed what I predicted. Her map looks a lot like theirs, maximizing the vote in Center City and its ring:

View code

ggplot(
  div_cp %>% 
    filter(candidate == "Yu, K")
) +
  geom_sf(aes(fill=pmin(100*pvote, 18)), color=NA) +
  theme_map_sixtysix() +
  scale_fill_viridis_c(
    "Percent of Vote", 
    labels=function(x) paste0(x, "%", ifelse(x>=18,"+",""))
  ) +
  expand_limits(fill=18)+
  ggtitle("Kay Yu's Results")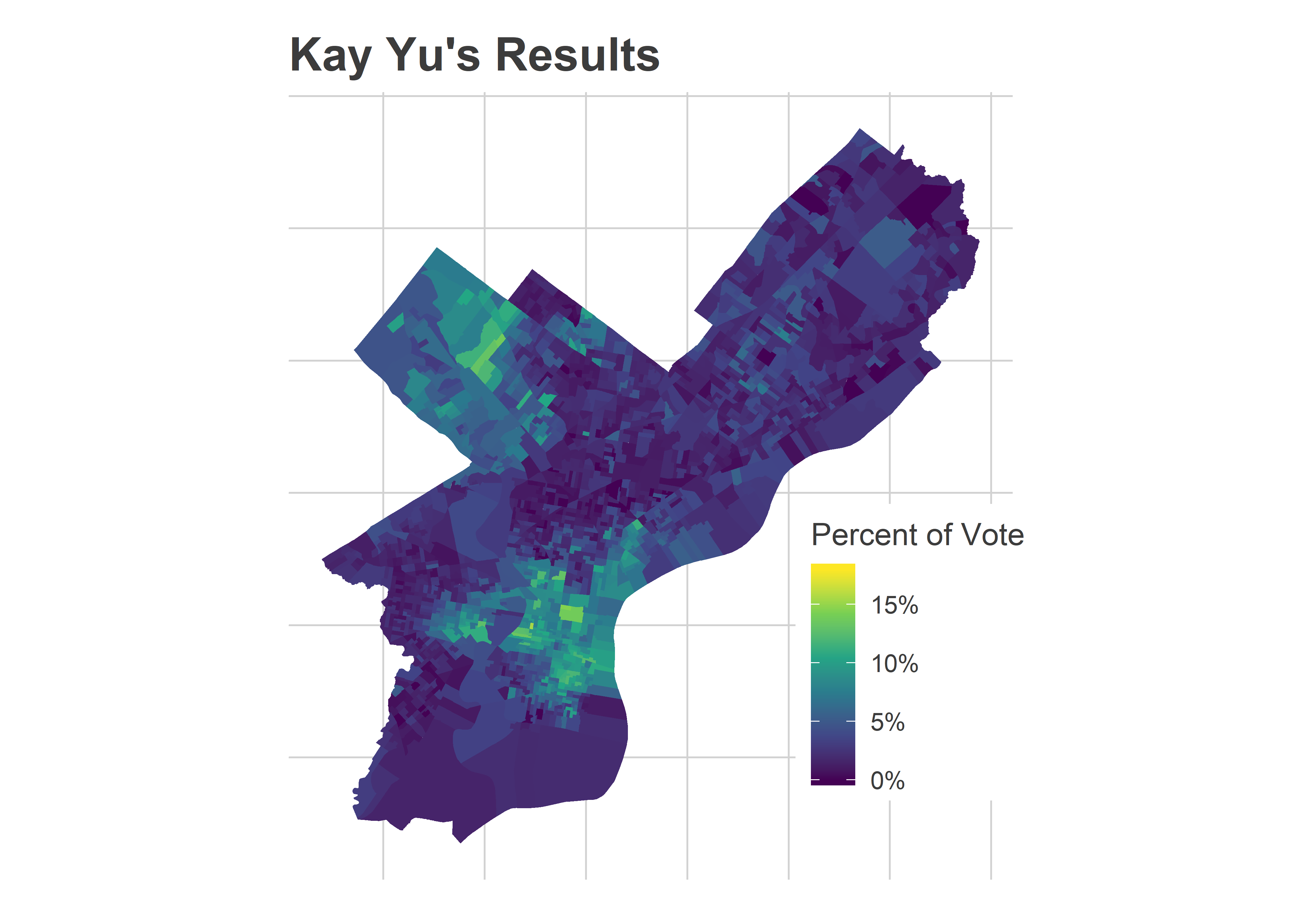

Yu presumably exploited the same strategies as Palmer, and Yu’s map might be what Palmer’s map would have looked like without the High Recommendation: a surprisingly strong showing that just falls short.

Finally, what is the direct effect of being Highly Recommended? How many people look that up before entering the booth, or grab the Inquirer, which listed the results? I don’t have a good way to know that, to disentangle that from the mediating, indirect pathways. And frankly, the winners probably don’t care whether their wins came from direct or mediating pathways, a win’s a win.

But that does lead me to…

The effect of Sample Ballots, Part 2

Two years ago, I partnered with the Bar Association to measure the effect of handing out their recommendations at polling places. This year, we decided not to randomize, but they still sent out nearly 100 volunteers to hand out recommendations outside of polling places. The Bar targeted polling places with high turnout, and allowed volunteers to self-select.

These are the flyers:

View code

knitr::include_graphics("PBA-Flyer-6.PNG")

The flyer is more aggressive than two years ago, with some serious UX design. How much effect did it have? The folks at the Bar sent me their assignments, so let’s dig in.

This analysis is more challenging than two years ago because we didn’t randomize polling place assignments. We might worry, for example, that the Bar Association’s volunteers would want to go close to their houses, and that those houses would be in places where the Highly Recommended candidates would already do well. Did that happen?

View code

vols <- read_csv("../../data/common_pleas/bar_assignments_2019.csv")
polling_places_to_divs <- read_csv("../../data/common_pleas/2019_Primary_Polling_Places.csv")

names(vols) <- tolower(names(vols))
names(polling_places_to_divs) <- tolower(names(polling_places_to_divs))

polling_places <- polling_places_to_divs %>% select(location, address) %>% 
  unique %>%
  mutate(place_id = 1:n())

polling_places_to_divs <- polling_places_to_divs %>%
  mutate(warddiv = sprintf("%02d-%02d", ward, division)) %>%
  left_join(polling_places)

divs <- st_read("../../data/gis/2019/Political_Divisions.shp",quiet=TRUE) %>% st_transform(2272)
polling_places_sf <- divs %>%
  mutate(warddiv = paste0(substr(DIVISION_N, 1, 2), "-", substr(DIVISION_N,3,4))) %>%
  left_join(polling_places_to_divs) %>%
  group_by(place_id) %>%
  summarise(geometry = st_union(geometry))

vols_to_divs <- vols %>% 
  left_join(polling_places_to_divs) 
if(any(is.na(vols_to_divs$ward))) stop("Missing Polling Place")

polling_places <- polling_places %>%
  left_join(vols %>% select(location, address, shift) %>% mutate(has_vol=TRUE)) %>%
  mutate(has_vol=ifelse(is.na(has_vol), FALSE, has_vol))

polling_places <- polling_places %>% left_join(polling_places_sf)

ggplot(polling_places) +
  geom_sf(aes(fill = has_vol), color="grey78") +
  scale_fill_manual(values=c("TRUE"=light_purple, "FALSE"="grey70"), guide=FALSE) +
  theme_map_sixtysix() +
  ggtitle("Where Bar volunteers went")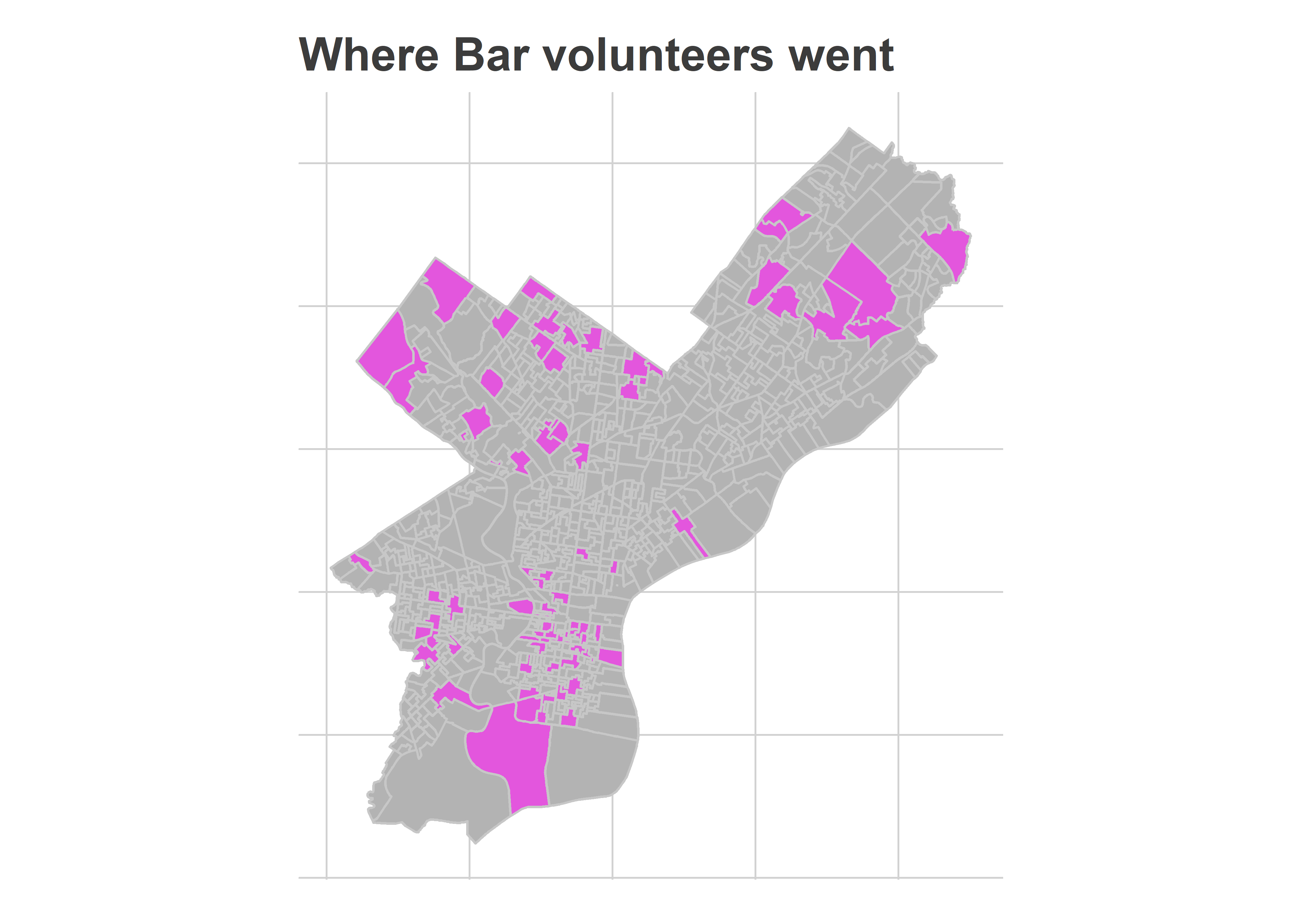

Yes and no. It’s not exactly a representative sample (vast sections of North Philly and the lower Northeast are missing), but it’s also not entirely Center City and its ring, which I worried. It was in the high-income wards that two years ago we found the lowest effect, because voters were already voting for Recommended candidates.

The divisions where they went were slightly non-representative: Highly Recommended candidates received 6.3% of the votes in Divisions that neighbored the volunteers, compared to 6.0% citywide. But that’s smaller than I might have worried.

View code

df_cp_pp <- df_cp %>% 
  left_join(polling_places_to_divs %>% select(warddiv, place_id)) %>%
  group_by(candidate, place_id) %>%
  summarise(votes = sum(Vote_Count))

neighbors <- st_intersection(
  polling_places_sf, 
  polling_places_sf %>% rename(place_id2 = place_id)
) %>%
  filter(place_id != place_id2)

neighbors <- neighbors %>%
  mutate(geometry_type = st_geometry_type(geometry)) %>%
  filter(!geometry_type %in% c("POINT", "MULTIPOINT")) %>%
  as.data.frame %>% select(place_id, place_id2)

df_neighbor <- neighbors %>%
  left_join(
    polling_places %>% select(place_id, has_vol), 
    by = c("place_id2" = "place_id")
  ) %>%
  rename(nb_has_vol = has_vol) %>%
  left_join(df_cp_pp, by=c("place_id2"="place_id")) %>%
  group_by(place_id, candidate) %>%
  summarise(
    votes_neighbor = sum(votes),
    neighbors=c(list(place_id2)),
    votes_neighbor_novol = sum(votes * !nb_has_vol)
  ) %>%
  group_by(place_id) %>%
  mutate(
    # pvote_neighbor = votes_neighbor / sum(votes_neighbor),
    pvote_neighbor_novol = votes_neighbor_novol / sum(votes_neighbor_novol)
  ) 

df_neighbor <- df_neighbor %>%
  left_join(df_cp_pp) %>%
  group_by(place_id) %>%
  mutate(pvote = votes/sum(votes))

df_neighbor <- df_neighbor %>%
  left_join(polling_places %>% as.data.frame() %>% select(place_id, has_vol, shift))

df_neighbor <- df_neighbor %>% left_join(ballot)

## Neighbor votes, for number above
test_summary <- df_neighbor %>%
  filter(has_vol) %>%
  group_by(candidate, philacommrec) %>%
  summarise(votes = sum(votes)) %>%
  group_by() %>%
  mutate(pvote = votes/ sum(votes)) %>%
  group_by(philacommrec) %>%
  summarise(`% Vote in volunteer divisions` = 100*mean(pvote))

control_summary <- df_neighbor %>% 
  filter(has_vol) %>%
  group_by(candidate, philacommrec) %>%
  summarise(votes = sum(pvote_neighbor_novol)) %>%
  group_by() %>%
  mutate(pvote = votes/ sum(votes)) %>%
  group_by(philacommrec) %>%
  summarise(`% Vote in neighboring divisions` = 100*mean(pvote))

overall_summary <- df_cp %>%
  group_by(candidate, philacommrec) %>%
  summarise(votes = sum(Vote_Count)) %>% 
  group_by() %>%
  mutate(pvote = votes/ sum(votes)) %>%
  group_by(philacommrec) %>%
  summarise(`% Vote citywide` = 100*mean(pvote))

knitr::kable(
  test_summary %>% 
    left_join(control_summary) %>% 
    left_join(overall_summary) %>%
    mutate(
      philacommrec = c("Not Recommended", "Recommended", "Highly Recommended")[philacommrec + 1]
    ) %>% rename("Recommendation" = philacommrec),
  digits=1
)

Recommendation	% Vote in volunteer divisions	% Vote in neighboring divisions	% Vote citywide
Not Recommended	1.7	1.8	1.9
Recommended	4.2	4.3	4.3
Highly Recommended	6.8	6.3	6.0

What was the effect of those volunteers? Let’s compare the highly-recommended candidates’ performance in volunteer divisions to their performance in neighboring divisions without volunteers.

View code

ggplot(
  df_neighbor %>% 
    filter(philacommrec == 2 & has_vol),
  aes(x = 100 * pvote_neighbor_novol, y=100*pvote)
) +
  geom_point(
    alpha = 0.5,
    pch=16,
    size=2,
    color=strong_purple
  ) +
  facet_wrap(~candidate) +
  coord_fixed() +
  geom_abline(slope=1, intercept=0) +
  scale_x_continuous("Percent of vote in neighboring polling places") +
  scale_y_continuous("Percent of vote in volunteer polling place") +
  expand_limits(x=0, y=0) +
  geom_smooth(method = lm, color="grey10")+
  theme_sixtysix() +
  ggtitle("Highly Recommended Candidates' performance\nwhere volunteers handed out recommendations")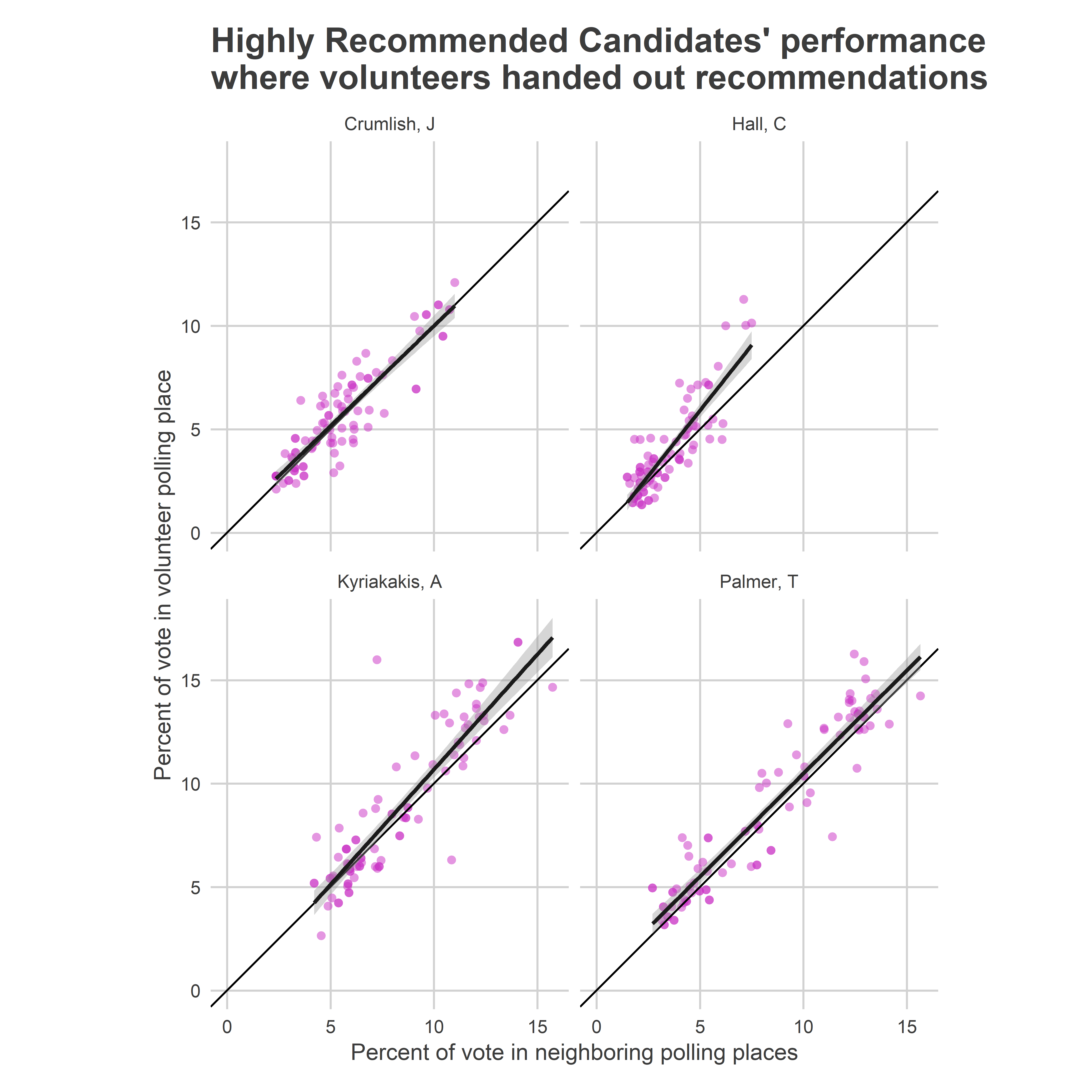

Each of the candidates did better in the polling places with volunteers than without them, with some evidence that the gap actually was bigger in places where they already were doing well.

On average, the difference between the percent of the vote earned in the volunteer divisions and the vote earned in neighboring divisions was half a percentage point for three of the candidates.

View code

df_neighbor %>% 
  filter(philacommrec == 2 & has_vol) %>%
  group_by(candidate) %>%
  summarise(
    pvote = 100 * mean(pvote),
    pvote_neighbor_novol = 100 * mean(pvote_neighbor_novol)
  ) %>%
  mutate(diff = pvote - pvote_neighbor_novol) %>%
  knitr::kable(
    digits = 2, 
    col.names = c("Candidate", "% Vote in volunteer divisions", "% Vote in neighboring divisions", "Difference")
  )

Candidate	% Vote in volunteer divisions	% Vote in neighboring divisions	Difference
Crumlish, J	5.67	5.53	0.15
Hall, C	3.90	3.41	0.49
Kyriakakis, A	8.75	8.26	0.49
Palmer, T	8.56	8.07	0.50

We can use regression (with candidate random effects) to measure the average effect of volunteers. Notice that since the target is itself a paired difference, the candidate random effects represent heterogeneous volunteer treatment effects: listings may effect candidates differently.

On average, the volunteers increased the gap between Highly Recommended and Not Recommended candidates by 0.48 percentage points versus neighboring divisions.

View code

library(lme4)
lmer_fit <- lmer(
  I(100 * (pvote - pvote_neighbor_novol)) ~ philacommrec + (1 | candidate),
  df_neighbor %>%
    filter(has_vol) %>%
    mutate(philacommrec = as.character(philacommrec))
)

# summary(lmer_fit)
knitr::kable(
  broom::tidy(lmer_fit) %>% 
    select(-group, -statistic) %>%
    mutate(term = c(
      "(Intercept)" = "Intercept (Effect of Volunteer on Not Recommended candidates)",
      "philacommrec1" = "Additional effect on Recommended candidates",
      "philacommrec2" = "Additional effect on Highly Recommended candidates",
      "sd_(Intercept).candidate" = "S.D. of candidate effects",
      "sd_Observation.Residual" = "S.D. of residual"
    )), 
  digits=2,
  col.name = c("Estimand", "Estimate", "Std. Error")
)

Estimand	Estimate	Std. Error
Intercept (Effect of Volunteer on Not Recommended candidates)	-0.07	0.09
Additional effect on Recommended candidates	-0.01	0.11
Additional effect on Highly Recommended candidates	0.48	0.15
S.D. of candidate effects	0.20	NA
S.D. of residual	1.12	NA

Note that this estimate is the average effect among the divisions where the volunteers actually went. If they are not representative of the city as a whole, then this wouldn’t estimate the average effect if we were to send volunteers everywhere. Specifically, if we were to send volunteers everywhere, we might expect the overall average effect to be higher, since these were the divisions

Is this effect comparable to our estimate two years ago? It’s hard to say. First, in the last election there were no Highly Recommended candidates. We found that Recommended candidates received no benefit from volunteers in wealthy divisions, largely because residents were voting for them already. We replicated that finding this time, but actually did find a statistically significant boost for Highly Recommended candidates.

Second, the size of 0.5 percentage points likely would have been smaller two years ago, just because of the number of open spots. This year, voters were selecting 6 judges, in 2017 they elected 9. The raw math of that means that winners receive less of the vote, so the same treatments will probably have smaller raw effects. In this analysis, the 0.48 percentage point effect was 1/11th of the 5.3% it took to win. In 2017, listings increased the gap between Recommended and Not Recommended candidates by 0.41 percentage points, which was about 1/10th of 4.1% needed to win.

Lessons Learned

This year, we elected zero Not Recommended judges. That’s a big achievement, and important not to overlook.

Most of that was luck. If a Not Recommended candidate were to end up at the top of the first column, they would probably still win. Our system is still stupid.

But, the Highly Recommended candidates did better than we’ve seen before. That was probably mostly thanks to those candidates capitalizing on the recommendations: Palmer clearly maximized its impact in a way that Hall and even winner Crumlish didn’t.

Handing out listings had a larger effect this time than we saw two years ago, and may be part of a pathway to electing Highly Recommended judges, but more important is the myriad other ways that the Highly Recommended candidates have to capitalize on the Recommendations.

June 8, 2019March 2, 2021

R Tutorial: How I crosswalk Philadelphia’s election data

Philadelphia’s past election results are all released based on past division boundaries. In order to make good historical comparisons, it’s necessary to apportion these old results into the modern boundaries. This post is a tutorial on how I use R’s GIS packages to crosswalk old data to present-day boundaries.

Note: All of the data and resources are available at https://github.com/jtannen/crosswalk. Just want the final crosswalked election data? You can find it in the outputs folder.

Note 2: I’ve turned this into an R package, available at https://github.com/jtannen/jaywalkr.

For GIS in R, I use the sf package, which is a tidyverse-friendly mapping library.

What is crosswalking?

What’s the challenge? Below is a map of the divisions in Philadelphia’s 5th Ward, using 2016 and 2019 boundaries.

library(sf)
library(dplyr)
library(tidyr)
library(ggplot2)

sixtysix_colors <- list(
  red="#D0445E",
  blue="#0077E0",
  purple="#C92EC4",
  green="#009871",
  orange="#9C7200",
  grey="#009871",
  light_red="#EE6178"
)

theme_map_sixtysix <- function(){ 
  ggthemes::theme_map() %+replace%
    theme(
      text = ggthemes::theme_fivethirtyeight()$text,
      title = ggthemes::theme_fivethirtyeight()$plot.title,
      panel.grid.major = element_line(color="grey90")
    )
}

divs_16 <- st_read("data/division_shapefiles/2016/2016_Ward_Divisions.shp") %>%
  rename(warddiv16 = WARD_DIVSN) %>%
  mutate(
    DIVSN = sprintf("%02d", DIVSN),
    WARD = sprintf("%02d", WARD)
  ) %>%
  st_transform(4326)
  
divs_19 <- st_read("data/division_shapefiles/2019/Political_Divisions.shp") %>%
  rename(warddiv19 = DIVISION_N) %>%
  mutate(WARD = substr(warddiv19, 1, 2))%>%
  st_transform(4326)
  
ggplot(
  divs_16 %>% filter(WARD == "05")
) +
    geom_sf(
    color = sixtysix_colors$light_red,
    size=2, 
    fill=NA
  ) + 
  geom_text(
    aes(x=X, y=Y, label = DIVSN),
    data = with(
      divs_16 %>% filter(WARD == "05"),
      data.frame(DIVSN, st_centroid(geometry) %>% st_coordinates())
    ),
    color=sixtysix_colors$light_red,
    size=4,
    fontface="bold"
  ) +
  geom_sf(
    data=divs_19 %>% filter(WARD == "05"),
    color = "black",
    size=1,
    fill=NA
  ) +
  geom_text(
    aes(x=X, y=Y, label = SHORT_DIV_),
    data = with(
      divs_19 %>% filter(WARD == "05"),
      data.frame(SHORT_DIV_, st_centroid(geometry) %>% st_coordinates())
    ),
    color="black",
    size=4
  ) +
  geom_text(
    aes(label=year, x=x, y=y, fontface=fontface, color=color),
    data=tribble(
      ~year, ~x, ~y, ~fontface, ~color,
      2016, -75.12607, 39.941, "bold", sixtysix_colors$light_red,
      2019, -75.12607, 39.943, "plain", "black"
    ),
    hjust=1
  ) +
  scale_color_identity(guide=FALSE) +
  theme_map_sixtysix() +
  ggtitle("Division change in Ward 5")

Notice that many of the boundaries changed. Five divisions were added: 05-30 through 05-34. Division 05-03 expanded down into 05-19. Division 05-26 shrank. If we were to naively compare 2016 and 2019 results by division id, we see that 05-21’s votes nosedived, while 05-34 went from 0 votes (it was non-existent) to a huge number. What we need to do instead is apportion the votes from the old boundaries to the new ones.

The challenge is that we don’t have the right data to perfectly make that decision. Look at 2016’s 05-21. It gets divided into 05-21, 05-33, and 05-34. Should we divide its votes evenly among the three? Should we apportion it based on the area of each division? By population?

Areal Weighting

A simple, common technique is to apportion values by area. We can calculate the area of each intersection, and give 2016’s votes to 2019 boundaries proportional to how much of its area lies in each (this is called “areal weighting”). We’ll reproject them to EPSG:2272 (the PA South State Plane) to get the most accurate areas:

areal_weights <- st_intersection(
  st_transform(divs_16, 2272), 
  st_transform(divs_19, 2272)
) %>% 
  mutate(area = st_area(geometry)) %>% 
  as.data.frame() %>% 
  select(warddiv16, warddiv19, area) %>% 
  group_by(warddiv16) %>% 
  mutate(prop_of_16 = as.numeric(area / sum(area))) 

areal_weights %>%
  filter(warddiv16 == "0521")

## # A tibble: 5 x 4
## # Groups:   warddiv16 [1]
##   warddiv16 warddiv19             area   prop_of_16
##      <fctr>    <fctr>      <S3: units>        <dbl>
## 1      0521      1802     712.1734 US_survey_foot^2 6.830801e-05
## 2      0521      0530    9891.1043 US_survey_foot^2	9.487038e-04
## 3      0521      0534 7279215.1422 US_survey_foot^2	6.981848e-01
## 4      0521      0533 1929128.9079 US_survey_foot^2	1.850321e-01
## 5      0521      0521 1206966.6049 US_survey_foot^2	1.157660e-01

The above shows us that Division 05-21 in 2016 was split up into five divisions for 2019. Two of them–18-02 and 05-30–look like noise; the areas are tiny and probably represent a trivial move in the boundary.

To apportion 2016’s votes to 2019 boundaries, we would give new division 05-34 69.8% of the votes, 05-33 18.5%, and 05-21 11.6%. Done.

Exercise: What assumptions make this apportionment valid? (answer in appendix)

Population Weighting

I usually do one better than areal weighting: population weighting. Instead of calculating the area of the intersection, I calculate the population living in each intersection. We then apportion 2016 counts proportionally to the population in each boundary. For example, 2019’s 05-34 lies along the Delaware River, and includes a vast industrial region. It probably represents many fewer votes than its area would suggest. Instead of using the area of each population, we could use the population.

We need fine-scale data to make this calculation. Luckily, the Census provides us with block-level populations every ten years.

phila_blocks <- st_read("data/census_blocks/tl_2010_42101_tabblock10.shp") %>%
  st_transform(4326)
  
## We'll only deal with centroids, since blocks are contained within divisions
phila_blocks <- st_centroid(phila_blocks)

phila_block_pops <- read.csv(
  "data/census_blocks/phila_block_pops.csv", 
  colClasses=c("character","numeric")
)

phila_blocks <- left_join(phila_blocks, phila_block_pops)

Here are the 2010 populations of the Census Blocks of the area.


ward_05_blocks <- sapply(
  phila_blocks %>% st_within(divs_19 %>% filter(WARD == "05")),
  length
) == 1
ward_05_blocks <- phila_blocks[ward_05_blocks,] %>%
  mutate(x = st_coordinates(geometry)[,1],
         y = st_coordinates(geometry)[,2])

ggplot(
  divs_16 %>% filter(WARD == "05")
) +
  geom_point(
    data = ward_05_blocks, 
    aes(x=x,y=y,size = pop10),
    alpha = 0.3,
    pch = 16,
    color=sixtysix_colors$blue
  ) +
  scale_size_area(guide=FALSE) +
  expand_limits(size=0) +
  geom_sf(
    color = sixtysix_colors$light_red,
    size=2, 
    fill=NA
  ) + 
  geom_text(
    aes(x=X, y=Y, label = DIVSN),
    data = with(
      divs_16 %>% filter(WARD == "05"),
      data.frame(DIVSN, st_centroid(geometry) %>% st_coordinates())
    ),
    color=sixtysix_colors$light_red,
    size=4,
    fontface="bold"
  ) +
  geom_sf(
    data=divs_19 %>% filter(WARD == "05"),
    color = "black",
    size=1,
    fill=NA
  ) +
  geom_text(
    aes(x=X, y=Y, label = SHORT_DIV_),
    data = with(
      divs_19 %>% filter(WARD == "05"),
      data.frame(SHORT_DIV_, st_centroid(geometry) %>% st_coordinates())
    ),
    color="black",
    size=4
  ) +
  geom_text(
    aes(label=year, x=x, y=y, fontface=fontface, color=color),
    data=tribble(
      ~year, ~x, ~y, ~fontface, ~color,
      2016, -75.12607, 39.941, "bold", sixtysix_colors$light_red,
      2019, -75.12607, 39.943, "plain", "black"
    ),
    hjust=1
  ) +
  scale_color_identity(guide=FALSE) +
  theme_map_sixtysix() +
  ggtitle("Division change in Ward 5", "Dots are 2010 Census Block Populations")

The goal is simple: to add up the blue dots inside of each intersection, and apportion votes that way.

get_pop_of_geoms <- function(g, idcol, blocks=phila_blocks){
  if(st_crs(g) != st_crs(blocks)) stop("g and blocks must have same crs.")
  intersection <- st_intersects(blocks, g)
  nmatch <- sapply(intersection, length)
  
  if(sum(blocks$pop10[nmatch==0]) > 0) stop("blocks weren't matched; population was lost.")
  if(any(nmatch > 1)) stop("blocks matched to multiple geometries. This shouldn't happen.")
  
  matches <- data.frame(
    blocki = (1:length(nmatch))[nmatch == 1], 
    gi = unlist(intersection)
  ) %>% mutate(
    block_id = blocks$GEOID10[blocki],
    g_id = g[[idcol]][gi]
  ) %>%
    left_join(
      blocks %>% as.data.frame %>% select(pop10, GEOID10),
      by = c("block_id"="GEOID10")
    ) %>%
    group_by(g_id) %>%
    summarise(pop10 = sum(pop10))
  
  if(sum(matches$pop10) != sum(blocks$pop10)) stop("Population was lost/added. Something's wrong.")
  
  names(matches)[1] <- idcol
  
  return(matches)
}

get_crosswalk <- function(g1, g2, idcol1, idcol2, blocks=phila_blocks){
  if(st_crs(g1) != st_crs(g2)) stop("g1 and g2 must have same crs.")
  g1$id1 <- g1[[idcol1]]
  g2$id2 <- g2[[idcol2]]
  
  intersection <- st_intersection(g1, g2)
  intersection <- intersection %>%
    mutate(id1_id2 = paste(id1, id2, sep="_")) %>%
    select(id1_id2, geometry)
  pop_of_intersection <- get_pop_of_geoms(intersection, "id1_id2", blocks)
  crosswalk <- pop_of_intersection %>%
    separate(id1_id2, c("id1", "id2"), sep = "_") %>%
    group_by(id1, id2) %>%
    summarise(pop10 = sum(pop10)) %>%
    group_by(id1) %>%
    mutate(frac_of_g1 = {if(sum(pop10) > 0) pop10/sum(pop10) else 1/n()}) %>%
    group_by(id2) %>%
    mutate(frac_of_g2 = {if(sum(pop10) > 0) pop10/sum(pop10) else 1/n()}) %>%
    group_by()
  
  names(crosswalk)[1:2] <- c(idcol1, idcol2)
  return(crosswalk)
}

crosswalk_16_19 <- get_crosswalk(divs_16, divs_19, "warddiv16", "warddiv19")
head(crosswalk_16_19)

## # A tibble: 6 x 5
##   warddiv16 warddiv19 pop10 frac_of_g1 frac_of_g2
##       <chr>     <chr> <dbl>      <dbl>      <dbl>
## 1      0101      0101   878          1          1
## 2      0102      0102   834          1          1
## 3      0103      0103   759          1          1
## 4      0104      0104  1006          1          1
## 5      0105      0105   807          1          1
## 6      0106      0106   762          1          1

What happened to 05-10 and 05-21, above?

crosswalk_16_19 %>% 
  filter(warddiv16 %in% c("0521", "0510"))

## # A tibble: 5 x 5
##   warddiv16 warddiv19 pop10 frac_of_g1 frac_of_g2
##       <chr>     <chr> <dbl>      <dbl>      <dbl>
## 1      0510      0510   390  0.8405172  0.4016478
## 2      0510      0530    74  0.1594828  0.1223140
## 3      0521      0521   716  0.3308688  1.0000000
## 4      0521      0533   936  0.4325323  1.0000000
## 5      0521      0534   512  0.2365989  1.0000000

The crosswalk says that 05-21 was split into 05-21, 33, and 34, in proportions of 0.33, 0.43, and 0.24. Notice that crosswalking back, it says that all of 2019’s 05-33 is contained in 2016’s 05-21, which is correct (frac_of_g2 = 1.0).

It says that 2019’s 05-30 is only 0.12 within 2016’s 05-10. Most of its population actually comes from that region to the West, which is smaller in area.

Exercise 2: What is the assumption(s) in using population-based weighting?

Finally, let’s crosswalk the raw data from 2016 forward to 2019 divisions. The folder data/raw_votes contains csv files of Philadelphia elections as downloaded directly from www.philadelphiavotes.com.

general_16 <- read.csv("data/raw_votes/2016_general.csv") %>%
  mutate(warddiv16 = paste0(sprintf("%02d", WARD), sprintf("%02d", DIVISION)))
head(general_16)

##   WARD DIVISION TYPE           OFFICE           CANDIDATE      PARTY VOTES
## 1    1        1    A ATTORNEY GENERAL            Write In                0
## 2    1        1    A ATTORNEY GENERAL       JOHN RAFFERTY REPUBLICAN     1
## 3    1        1    A ATTORNEY GENERAL        JOSH SHAPIRO DEMOCRATIC     6
## 4    1        1    A  AUDITOR GENERAL            Write In                0
## 5    1        1    A  AUDITOR GENERAL EUGENE A DEPASQUALE DEMOCRATIC     5
## 6    1        1    A  AUDITOR GENERAL          JOHN BROWN REPUBLICAN     0
##   warddiv16
## 1      0101
## 2      0101
## 3      0101
## 4      0101
## 5      0101
## 6      0101

To crosswalk, we will apportion each 2016 division’s votes to 2019 boundaries proportional to the 2016 fraction of population.

general_16_crosswalked <- general_16 %>%
  left_join(crosswalk_16_19, by = "warddiv16") %>%
  group_by(TYPE, OFFICE, CANDIDATE, PARTY, warddiv19) %>%
  summarise(VOTES = sum(VOTES * frac_of_g1))

head(general_16_crosswalked)

## # A tibble: 6 x 6
## # Groups:   TYPE, OFFICE, CANDIDATE, PARTY [1]
##     TYPE           OFFICE     CANDIDATE      PARTY warddiv19 VOTES
##   <fctr>           <fctr>        <fctr>     <fctr>     <chr> <dbl>
## 1      A ATTORNEY GENERAL JOHN RAFFERTY REPUBLICAN      0101     1
## 2      A ATTORNEY GENERAL JOHN RAFFERTY REPUBLICAN      0102     1
## 3      A ATTORNEY GENERAL JOHN RAFFERTY REPUBLICAN      0103     3
## 4      A ATTORNEY GENERAL JOHN RAFFERTY REPUBLICAN      0104     5
## 5      A ATTORNEY GENERAL JOHN RAFFERTY REPUBLICAN      0105     2
## 6      A ATTORNEY GENERAL JOHN RAFFERTY REPUBLICAN      0106     0

We’re done! We have 2016’s results in 2019 boundaries.

Note: We could probably do even one better, and geocode the addresses of where people actually voted, using data from the voter file for each year. Maybe I’ll get around to that one day…

Crosswalking all the data

Just for finality, let’s loop through all years and store the outputs. Sounds easy, but… oof.

I’ve only been able to find shapefiles for divisions from a handful of years. The amazing folks at Azavea and the Commissioners’ Office have put together a batch of historical division boundaries, but even their herculean efforts don’t perfectly cover all recent elections. I’ve only got boundaries for 2005, 2008-2013, 2016, and 2019. For each election, I’ve chosen the boundaries that appear to fit best based on divisions being created or destroyed, but I can’t know how pesty boundary changes might affect these numbers.

Note: Have more complete division boundaries? Want to be a hero and create them from the text description of boundaries? Let me know!

crosswalk_years <- list.dirs("data/division_shapefiles", full.names = F)

for(crosswalk_year in crosswalk_years[!crosswalk_years %in% c("", "2019")]){
  crosswalk_year2 <- substr(crosswalk_year, 3, 4)
  div_dir <- sprintf("data/division_shapefiles/%s", crosswalk_year)
  div_path <- list.files(div_dir, pattern = ".*\\.shp$", full.names = TRUE)
  g1 <- st_read(div_path) %>% 
    mutate(warddiv = paste0(sprintf("%02d", WARD), sprintf("%02d", DIVSN))) %>%
    st_transform(4326)
  
  idcol <- paste0("warddiv", crosswalk_year2)
  names(g1)[names(g1) == "warddiv"] <- idcol
  
  crosswalk <- get_crosswalk(g1, divs_19, idcol, "warddiv19")
  write.csv(
    crosswalk, 
    file=paste0("outputs/", "crosswalk_", crosswalk_year2, "_to_19.csv"),
    row.names = FALSE
  )
}

use_crosswalk <- tribble(
  ~year, ~election, ~crosswalk_year,
    2002, "primary", 2005,
    2002, "general", 2005,
    2003, "primary", 2005,
    2003, "general", 2005,
    2004, "primary", 2005,
    2004, "general", 2005,
    2005, "primary", 2005,
    2005, "general", 2005,
    2006, "primary", 2005,
    2006, "general", 2005,
    2007, "primary", 2005,
    2007, "general", 2005,
    2008, "primary", 2008,
    2008, "general", 2008,
    2009, "primary", 2008, # broken
    2009, "general", 2008, # broken
    2010, "primary", 2009,
    2010, "general", 2011,
    2011, "primary", 2011,
    2011, "general", 2011,
    2012, "primary", 2011,
    2012, "general", 2012,
    2013, "primary", 2013,
    2013, "general", 2013,
    2014, "primary", 2016, 
    2014, "general", 2016,
    2015, "primary", 2016,
    2015, "general", 2016,
    2016, "primary", 2016,
    2016, "general", 2016,
    2017, "primary", 2016,
    2017, "general", 2016,
    2018, "primary", 2019,
    2018, "general", 2019
)

fix_colnames <- function(df){
  ## 2018 general results changed all the column names...
  replace_name <- function(df, oldname, newname){
    names(df)[names(df) == oldname] <- newname
    return(df)
  }
  
  df <- df %>% 
    replace_name("CATEGORY", "OFFICE") %>%
    replace_name("SELECTION", "CANDIDATE") %>%
    replace_name("VOTE.COUNT", "VOTES")
  return(df)
}


ALLOW_MISTAKES <- TRUE
VERBOSE <- FALSE
elections_with_mistakes <- data.frame()

for(i in 1:nrow(use_crosswalk)){
  if(VERBOSE) print(use_crosswalk[i,])
  
  year <- use_crosswalk$year[i]
  election <- use_crosswalk$election[i]
  crosswalk_year <- use_crosswalk$crosswalk_year[i]
  
  election_df <- read.csv(sprintf("data/raw_votes/%s_%s.csv", year, election))
  election_df <- fix_colnames(election_df)
  election_df <- election_df %>% 
    mutate(warddiv = paste0(sprintf("%02d", WARD), sprintf("%02d", DIVISION)))
  
  if(crosswalk_year == "2019"){
    election_df_19 <- election_df %>% rename(warddiv19 = warddiv)
    
    missing_g1 <- unique(election_df$warddiv)[!(unique(election_df$warddiv) %in% divs_19$warddiv19)]
    missing_g2 <- divs_19$warddiv19[!(divs_19$warddiv19 %in% unique(election_df$warddiv))]
  } else {
    idcol <- paste0("warddiv", substr(crosswalk_year, 3, 4))
    
    crosswalk <- read.csv(
      sprintf("outputs/crosswalk_%s_to_19.csv", substr(crosswalk_year, 3, 4)),
      colClasses = c(rep("character", 2), rep("numeric", 3))
    )  
    
    election_df_19 <- election_df %>%
      left_join(crosswalk, by=c("warddiv"=idcol)) %>%
      group_by(TYPE, OFFICE, CANDIDATE, PARTY, warddiv19) %>%
      summarise(VOTES = sum(VOTES * frac_of_g1))
    
    missing_g1 <- unique(election_df$warddiv)[!(unique(election_df$warddiv) %in% unique(crosswalk[,idcol]))]
    missing_g2 <- unique(crosswalk[,idcol])[!(unique(crosswalk[,idcol]) %in% unique(election_df$warddiv))]
  }
  

  if(length(missing_g1) > 0 || length(missing_g2) > 0){
    if(!ALLOW_MISTAKES) stop("Votes mismatch. Something went wrong.")
    elections_with_mistakes <- bind_rows(
      elections_with_mistakes, 
      data.frame(
        year=year, 
        election=election, 
        lost_votes=sum(election_df$VOTES) - sum(election_df_19$VOTES),
        total_votes = sum(election_df$VOTES),
        g1_missing_from_crosswalk=paste(missing_g1, collapse=","),
        crosswalk_missing_from_g1=paste(missing_g2, collapse=",")
      )
    )
  }
  
  write.csv(
    election_df_19, 
    file=sprintf("outputs/%s_%s_crosswalked_to_19.csv", year, election),
    row.names=FALSE
  )
}

print(elections_with_mistakes)

##   year election lost_votes total_votes g1_missing_from_crosswalk   crosswalk_missing_from_g1
## 1 2009  primary          0     1564872            4923,4924,4925                          
## 2 2009  general          0     1816570            4923,4924,4925                          
## 3 2018  primary          0     1305757       1818,0532,0534,0533

Notice above the three elections with flagged mistakes. For the 2009 results, the 2008 crosswalk that I used was expecting three divisions that weren’t actually in the 2009 results. This is a problem; it means that I over-apportioned those votes somewhere else. The boundaries for 2009 aren’t any better, six divisions are missing. This isn’t the end of the world, three out of 1,681 divisions isn’t terrible. And the ward-level results will still be right. But don’t trust the division-level results for the 49th ward in 2009.

Similarly, the 2018 primary had two divisions that weren’t in the 2016 map, 05-30 and 05-31, but was missing four divisions that were used in the general: 18-18, 05-32, 05-33, and 05-34. I’ve used the 2019 boundaries, to avoid losing votes. Instead, 18-18 et al will be assumed to have 0 votes (which isn’t great either).

The fact that only these three elections are flagged isn’t dispositive proof that the other crosswalks were perfect: the boundaries could have moved without creating or removing division numbers, which is all that we’re checking.

I’ll keep looking for shapefiles, and will update the repo as I find them, but for the time being this is probably the best we can do.

That’s it!

We’ve created our crosswalks.

You can download the results from the outputs folder.

You may be uncomfortable with the simplicity of the assumptions above. This method usually does a darn good job of getting sensible data, but you might imagine some extensions:

– Using annual voter file weights instead of Decennial Census populations.

– A model-based Bayesian approach that uses similarities in voting patterns across years to guess which votes came from where. You could additionally use race and income data, which is released by the census at the Block level. These methods risk the Ecological Fallacy, but not in a worse way than what we’re already doing.

Answers to Exercises

What assumptions make the areal apportionment valid? It assumes that the value was spread uniformly in space in the original boundaries. For example, apportioning 2016 votes to 2019 boundaries using areal weighting assumes that the votes per mile in 2016 was evenly spread within each division (although it will obviously be different for different divisions).

What assumptions make the population apportionment valid? It assumes that the population is concentrated at the centroid of the block or that the blocks are entirely contained within one division (since we only use the centroids) and that the 2010 population is proportional to the target metric. The first is true in our case: divisions don’t split blocks, so blocks are entirely contained in divisions. The second is wrong, but much less wrong than the areal assumption: votes are more proportional to population than they are to area. We could make this better by using the correct year’s population if we had it, or using voting-age population or registered voters instead of census population, but this does a pretty darn good job.